
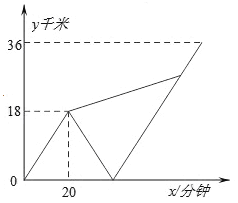
【题目】甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为t(分钟).y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题:
(1)电动车的速度为 千米/分钟;
(2)甲步行所用的时间为 分;
(3)求乙返回到学校时,甲与学校相距多远?
科目:初中数学 来源: 题型:
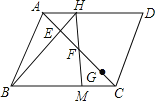
【题目】如图,ABCD的面积为20,点E,F,G为对角线AC的四等分点,连接BE并延长交AD于H,连接HF并延长交BC于点M,则![]() 的面积为
的面积为![]()
![]()
A. 10 B. ![]() C. 4 D. 5
C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两种型号的机器加工同一种零件,已知A型机器比B型机器每小时多加工20个零件,A型机器加工400个零件所用时间与B型机器加工300个零件所用时间相同.A型机器每小时加工零件的个数_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2 .
上述4个判断中,正确的是( )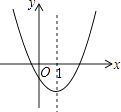
A.①②
B.①④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点. 
(1)试判断AB、AC之间的大小关系,并给出证明;
(2)在上述题设条件下,当△ABC为正三角形时,点E是否AC的中点?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△AOB中,∠AOB=90°,OA=3,OB=4.将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑩的直角顶点的坐标为 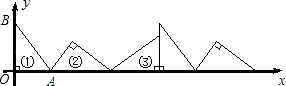
查看答案和解析>>
科目:初中数学 来源: 题型:
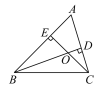
【题目】如图,在△ABC中,BD是AC边上的高,CE是AB边上的高,BD与CE相交于点O,则∠ABD___∠ACE(填“>”“<”或“=”),∠A+∠DOE=___度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,在以O为原点的平面直角坐标系中,抛物线y= ![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C(0,﹣1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<﹣1,
x2+bx+c与x轴交于A、B两点,与y轴交于点C(0,﹣1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<﹣1,
(1)求抛物线对应的二次函数的解析式;
(2)若D为抛物线y= ![]() x2+bx+c上一动点,是否存在直线l使得点D到直线l的距离与OD的长恒相等?若存在,求出此时t的值;
x2+bx+c上一动点,是否存在直线l使得点D到直线l的距离与OD的长恒相等?若存在,求出此时t的值;
(3)如图2,若E、F为上述抛物线上的两个动点,且EF=8,线段EF的中点为M,求点M纵坐标的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com