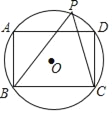
【题目】如图，矩形ABCD内接于⊙O，点P是
上一点，连接PB、PC，若AD=2AB，则cos∠BPC的值为（ ）
A. 
B. 
C. 
D. 
全能测控一本好卷系列答案科目：初中数学 来源： 题型：
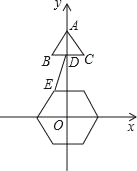
【题目】如图，已知边长为2的正三角形ABC顶点A的坐标为（0，6），BC的中点D在y轴上，且在点A下方，点E是边长为2、中心在原点的正六边形的一个顶点，把这个正六边形绕中心旋转一周，在此过程中DE的最小值为（ ）
A. 3 B. 4﹣
C. 4 D. 6﹣2
查看答案和解析>>
科目：初中数学 来源： 题型：
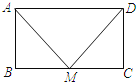
【题目】如图，已知点M为矩形ABCD中边BC的中点，若要使
为等腰直角三角形，则再须添加一条件；那么在下列给出的条件中，错误的是
A. 
B. AM是
的平分线
C. AM：
：
D. AB：
：
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，点P是线段AD上一动点，O为BD的中点，PO的延长线交BC于点Q。
（1）求证：OP=OQ；
（2）若AD=8cm，AB=6cm，P从点A出发，以1cm/秒的速度向点D运动（不与点D重合），设点P运动时间为t秒，请用t表示PD的长；并求当t为何值时，四边形PBQD是菱形。
查看答案和解析>>
科目：初中数学 来源： 题型：
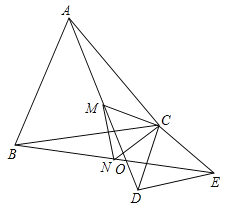
【题目】已知：如图，
、
都是等腰三角形，且
，
，
，
、
相交于点
，点
、
分别是线段、的中点．以下4个结论：①
；②
；③
是等边三角形；④连
，则平分
以上四个结论中正确的是：______．（把所有正确结论的序号都填上）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市扶贫办在精准扶贫工作中，组织30辆汽车装运花椒、核桃、甘蓝向外地销售．按计划30辆车都要装运，每辆汽车只能装运同一种产品，且必须装满，根据下表提供的信息，解答以下问题：
产品名称 | 核桃 | 花椒 | 甘蓝 |
每辆汽车运载量（吨） | 10 | 6 | 4 |
每吨土特产利润（万元） | 0.7 | 0.8 | 0.5 |
若装运核桃的汽车为x辆，装运甘蓝的车辆数是装运核桃车辆数的2倍多1，假设30辆车装运的三种产品的总利润为y万元．
(1)求y与x之间的函数关系式；
(2)若装花椒的汽车不超过8辆，求总利润最大时，装运各种产品的车辆数及总利润最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）已知
，点P在OA上，且
，点P关于直线OB的对称点是Q，则
________．
（2）已知，点P在
的内部，
，点
和点P关于OA对称，点
和点P关于OB对称，则、O、三点构成的三角形是________三角形，其周长为________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，⊙O是△ABC的外接圆，AB是⊙O的直径，D为⊙O上一点，OD⊥AC，垂足为E，连接BD.
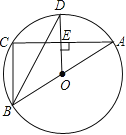
(1)求证：BD平分∠ABC；
(2) 当∠ODB=30°时，求证：BC=OD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
