
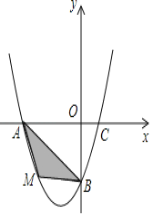
����Ŀ����ƽ��ֱ������ϵ�У���֪�����߾���A(��2��0)��B(0����2)��C(1��0)���㣮
��1���������ߵĽ���ʽ��
��2������MΪ������������������һ���㣬��M�ĺ�����Ϊm����AMB�����ΪS����S����m�ĺ�����ϵʽ�������S�����ֵ��
��3������P���������ϵĶ��㣬��Q��ֱ��y����x�ϵĶ��㣬�ж��м���λ���ܹ�ʹ�õ�P��Q��B��OΪ������ı���Ϊƽ���ı��Σ�ֱ��д����Ӧ�ĵ�Q�����꣮
���𰸡���1��y��x2+x��2����2��S����m2��2m����2��m��0����S�����ֵΪ1����3����Q����Ϊ��(��2��2)��(��1+![]() ��1��
��1��![]() )��(��1��
)��(��1��![]() ��1+
��1+![]() )��(2����2)��
)��(2����2)��
��������
��1����������ߵĺ�������ʽΪ��y��ax2+bx+c����A��B��C�������y��ax2+bx+c���з��������a��b��c��ֵ���ɵô𰸣�
��2����ͼ1������M��y���ƽ���߽�AB�ڵ�D��M��ĺ�����Ϊm���ҵ�M�ڵ��������������ϣ���M�������Ϊ��m��m2+m��2������2��m��0����A��B��������ֱ��AB�Ľ���ʽΪy����x��2�����D������Ϊ��m����m��2�����������MD�ij��ȣ���һ�������MAB�����S����m�ĺ�����ϵʽ�����ݶ��κ��������ʼ�����������ֵ��
��3����P��x��x2+x��2������������ۣ��ٵ�OBΪ��ʱ������ƽ���ı��ε�����֪PQ��OB����PQ��OB����Q��x����x�������г�����x�ķ��̣����������Q�����ꣻ�ڵ�BOΪ�Խ���ʱ��OQ��BP��A��PӦ���غϣ�OP��2���ı���PBQOΪƽ���ı��Σ���BQ��OP��2��Q������Ϊ2������д����Q�����꣮
��1����������ߵĺ�������ʽΪ��y��ax2+bx+c��
��A����2��0����B��0����2����C��1��0��������룬�� ��
��
��ã�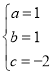 ��
��
��˺�������ʽΪ��y��x2+x��2��
��2����ͼ������M��y���ƽ���߽�AB�ڵ�D��
��M��ĺ�����Ϊm���ҵ�M�ڵ��������������ϣ�
����M���������m��m2+m��2������2��m��0��
��ֱ��AB�Ľ���ʽΪy��kx��2��
��A����2��0������ã�-2k-2=0��
��ã�k����1��
��ֱ��AB�Ľ���ʽΪy����x��2��
��MD��y�ᣬ
���D��������m����m��2����
��MD����m��2����m2+m��2������m2��2m��
��S��MAB��S��MDA+S��MDB
��![]() MDOA
MDOA
��![]() ��2��m2��2m��
��2��m2��2m��
����m2��2m
������
�ߩ�2��m��0��
�൱m����1ʱ��S��MAB�����ֵ1��

����������S����m�ĺ�����ϵʽ��S����m2��2m����2��m��0����S�����ֵΪ1��
��3����P��x��x2+x��2����
����ͼ����OBΪ��ʱ������ƽ���ı��ε�����֪PQ��OB����PQ��OB��
��Q�ĺ��������P�ĺ����꣬
��ֱ�ߵĽ���ʽΪy����x��
��Q��x����x����
��PQ��OB����|��x����x2+x��2��|��2��
��|��x2��2x+2|��2��
����x2��2x+2��2ʱ��x1��0���������⣬��ȥ����x2����2��
��Q����2��2����
����x2��2x+2����2ʱ��x1����1+![]() ��x2����1��
��x2����1��![]() ��
��
��Q����1+![]() ��1��
��1��![]() ����1��
����1��![]() ��1+
��1+![]() ����
����
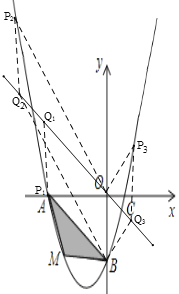
����ͼ����BOΪ�Խ���ʱ��OQ��BP��
��ֱ��AB�Ľ���ʽΪy=-x-2��ֱ��OQ�Ľ���ʽΪy=-x��
��A��P�غϣ�OP��2���ı���PBQOΪƽ���ı��Σ�
��BQ��OP��2����Q�ĺ�����Ϊ2��
��x=2����y����x��y=-2��
��Q��2����2����

������������Q����������2��2����1+![]() ��1��
��1��![]() ����1��
����1��![]() ��1+
��1+![]() ����2����2����
����2����2����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���![]() �У���
�У���![]() �ڱ�
�ڱ�![]() �ϣ�
�ϣ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��������ı���
��������ı���![]() �����֮��Ϊ___
�����֮��Ϊ___
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����C���߶�AB��һ�㣬AC��![]() AB��BCΪ��O��ֱ����
AB��BCΪ��O��ֱ����
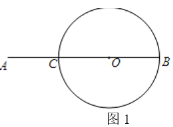
��1����ͼ1ֱ��BC�Ϸ���Բ������һ��P��ʹ��PA��PB�����ó߹���ͼ��������ͼ�ۼ�����Ҫ��д������
��2������PA����֤��PA�ǡ�O�����ߣ�
��3���ڣ�1���������£�����PC��PB����PAB��ƽ���߷ֱ�PC��PB�ڵ�D��E����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
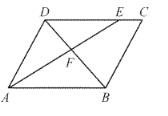
����Ŀ���ı���ABCD�ڽ��ڡ�O��ACΪ�Խ��ߣ���ACB����ACD
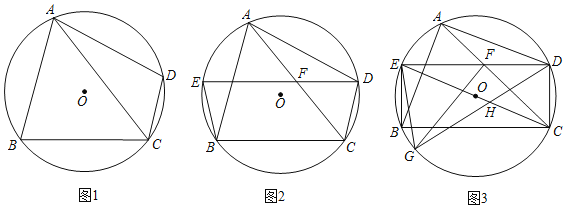
��1����ͼ1����֤��AB��AD��
��2����ͼ2����E��AB���ϣ�DE��AC�ڵ�F������BE��BE��DF����֤��DF��DC��
��3����ͼ3���ڣ�2���������£���G��BC���ϣ�����DG����CE�ڵ�H������GE��GF����DE��BC��EG��GH��5��S��DFG��9����BC�ߵij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��2x2+bx��6��ͼ����(2����6)����������κ�����x�ύ��A��B���㣬��y�ύ�ڵ�C�������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
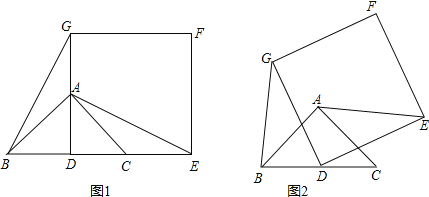
����Ŀ����ͼ1����֪![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�![]() ����D��BC���е�
����D��BC���е�![]() ��������DEFG��ʹ��A��C�ֱ���DG��DE�ϣ�����AE��BG��
��������DEFG��ʹ��A��C�ֱ���DG��DE�ϣ�����AE��BG��
![]() �Բ����߶�BG��AE��������ϵ��______��
�Բ����߶�BG��AE��������ϵ��______��
![]() ��������DEFG�Ƶ�D��ʱ�뷽����ת
��������DEFG�Ƶ�D��ʱ�뷽����ת![]() ��
��
![]() �ж�
�ж�![]() �еĽ����Ƿ���Ȼ������������ͼ2֤����Ľ��ۣ�
�еĽ����Ƿ���Ȼ������������ͼ2֤����Ľ��ۣ�
![]() ��
��![]() ����AEȡ���ֵʱ����AF��ֵ��
����AEȡ���ֵʱ����AF��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
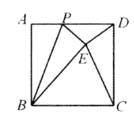
����Ŀ����֪������![]() �ı߳�Ϊ1��
�ı߳�Ϊ1��![]() Ϊ����
Ϊ����![]() �ϵĶ��㣨�����
�ϵĶ��㣨�����![]() �غϣ�����
�غϣ�����![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�Ϊ
�ĶԳƵ�Ϊ![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �ǵ���������ʱ��
�ǵ���������ʱ��![]() ��ֵΪ__________��
��ֵΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����߶�ACΪ�Խ��ߵ��ı���ABCD(�����ĸ�����A��B��C��D��˳ʱ�뷽������)����֪AB��BC��CD����ABC��100������CAD��40�������BCD�Ķ���Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ӽص��ҵ���A��B��C������ͬ�Ĺ�����·��Ϊ�˽���߷��ڼ���������·�ϵĹ������Ӽص��ҵص���ʱ�������ÿ����·�����ѡȡ��500����εĹ��������ռ�����Щ��εĹ�������ʱ����λ�����ӣ������ݣ�ͳ�����£�
��������ʱ ��������ʱ��Ƶ�� ��· |
|
|
|
| �ϼ� |
A | 59 | 151 | 166 | 124 | 500 |
B | 50 | 50 | 122 | 278 | 500 |
C | 45 | 265 | 167 | 23 | 500 |
��߷��ڼ䣬����_________������A������B������C������·�ϵĹ��������Ӽص��ҵ�����ʱ������45�������Ŀ��������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com