
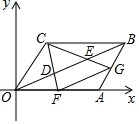
 如图,平面直角坐标系中O是原点,?ABCD的顶点A,C的坐标分别是(8,0),(3,4),点D,E把线段OB三等分,延长CD、CE分别交OA、AB于点F,G,连接FG.则下列结论:
如图,平面直角坐标系中O是原点,?ABCD的顶点A,C的坐标分别是(8,0),(3,4),点D,E把线段OB三等分,延长CD、CE分别交OA、AB于点F,G,连接FG.则下列结论:分析 ①证明△CDB∽△FDO,列比例式得:$\frac{BC}{OF}=\frac{BD}{OD}$,再由D、E为OB的三等分点,则$\frac{BD}{OD}$=$\frac{2}{1}=2$,可得结论正确;
②如图2,延长BC交y轴于H证明OA≠AB,则∠AOB≠∠EBG,所以△OFD∽△BEG不成立;
③如图3,利用面积差求得:S△CFG=S?OABC-S△OFC-S△OBG-S△AFG=12,根据相似三角形面积的比等于相似比的平方进行计算并作出判断;
④根据勾股定理进行计算OB的长,根据三等分线段OB可得结论.
解答  解:①∵四边形OABC是平行四边形,
解:①∵四边形OABC是平行四边形,
∴BC∥OA,BC=OA,
∴△CDB∽△FDO,
∴$\frac{BC}{OF}=\frac{BD}{OD}$,
∵D、E为OB的三等分点,
∴$\frac{BD}{OD}$=$\frac{2}{1}=2$,
∴$\frac{BC}{OF}=2$,
∴BC=2OF,
∴OA=2OF,
∴F是OA的中点;
所以①结论正确;
②如图2,延长BC交y轴于H,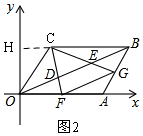
由C(3,4)知:OH=4,CH=3,
∴OC=5,
∴AB=OC=5,
∵A(8,0),
∴OA=8,
∴OA≠AB,
∴∠AOB≠∠EBG,
∴△OFD∽△BEG不成立,
所以②结论不正确;
③由①知:F为OA的中点,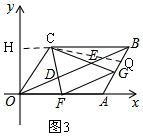
同理得;G是AB的中点,
∴FG是△OAB的中位线,
∴FG=$\frac{1}{2}OB$,FG∥OB,
∵OB=3DE,
∴FG=$\frac{3}{2}$DE,
∴$\frac{FG}{DE}$=$\frac{3}{2}$,
过C作CQ⊥AB于Q,
S?OABC=OA•OH=AB•CQ,
∴4×8=5CQ,
∴CQ=$\frac{32}{5}$,
S△OCF=$\frac{1}{2}$OF•OH=$\frac{1}{2}$×4×4=8,
S△CGB=$\frac{1}{2}$BG•CQ=$\frac{1}{2}$×$\frac{5}{2}$×$\frac{32}{5}$=8,
S△AFG=$\frac{1}{2}$×4×2=4,
∴S△CFG=S?OABC-S△OFC-S△OBG-S△AFG=8×4-8-8-4=12,
∵DE∥FG,
∴△CDE∽△CFG,
∴$\frac{{S}_{△CDE}}{{S}_{△CFG}}$=$(\frac{DE}{FG})^{2}$=$\frac{4}{9}$,
∴$\frac{{S}_{四边形DEGF}}{{S}_{△CFG}}$=$\frac{5}{9}$,
∴$\frac{{S}_{四边形DEGF}}{12}=\frac{5}{9}$,
∴S四边形DEGF=$\frac{20}{3}$;
所以③结论正确;
④在Rt△OHB中,由勾股定理得:OB2=BH2+OH2,
∴OB=$\sqrt{{4}^{2}+(3+8)^{2}}$=$\sqrt{137}$,
∴OD=$\frac{\sqrt{137}}{3}$,
所以④结论不正确;
故本题结论正确的有:①③;
故答案为:①③.
点评 本题是四边形的综合题,考查了平行四边形的性质、图形与坐标特点、勾股定理、三角形的中位线定理、三角形相似的性质和判定、平行四边形和三角形面积的计算等知识,难度适中,熟练掌握平行四边形和相似三角形的性质是关键.


科目:初中数学 来源: 题型:解答题
 如图,A、B两个村庄之间有一个池塘,A村到公路CD的距离AC=700米,若BC═600米,∠BCD=30°,试求A、B两个村庄之间的距离(结果保留根号).
如图,A、B两个村庄之间有一个池塘,A村到公路CD的距离AC=700米,若BC═600米,∠BCD=30°,试求A、B两个村庄之间的距离(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
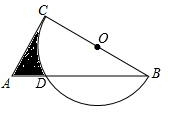 如图,Rt△ABC中,∠ACB=90°,AB=6,AC=3,以BC为直径的半圆交AB于点D,则阴影部分的面积为$\frac{45}{16}$$\sqrt{3}$+$\frac{9π}{80}$.
如图,Rt△ABC中,∠ACB=90°,AB=6,AC=3,以BC为直径的半圆交AB于点D,则阴影部分的面积为$\frac{45}{16}$$\sqrt{3}$+$\frac{9π}{80}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,点E,F分别是AD,BC边上的点,且AE=CF.
如图,在矩形ABCD中,点E,F分别是AD,BC边上的点,且AE=CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com