
【题目】阅读下列材料:
小明遇到一个问题:在![]() 中,
中,![]() ,
,![]() ,
,![]() 三边的长分别为
三边的长分别为![]() 、
、![]() 、
、![]() ,求
,求![]() 的面积.
的面积.
小明是这样解决问题的:如图①所示,先画一个正方形网格(每个小正方形的边长为![]() ),再在网格中画出格点
),再在网格中画出格点![]() (即
(即![]() 三个顶点都在小正方形的顶点处),从而借助网格就能计算出
三个顶点都在小正方形的顶点处),从而借助网格就能计算出![]() 的面积.他把这种解决问题的方法称为构图法.
的面积.他把这种解决问题的方法称为构图法.
参考小明解决问题的方法,完成下列问题:
(![]() )图
)图![]() 是一个
是一个![]() 的正方形网格(每个小正方形的边长为
的正方形网格(每个小正方形的边长为![]() ) .
) .
①利用构图法在答卷的图![]() 中画出三边长分别为
中画出三边长分别为![]() 、
、![]() 、
、![]() 的格点
的格点![]() .
.
②计算①中![]() 的面积为__________.(直接写出答案)
的面积为__________.(直接写出答案)
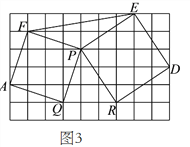
(![]() )如图
)如图![]() ,已知
,已知![]() ,以
,以![]() ,
,![]() 为边向外作正方形
为边向外作正方形![]() ,
,![]() ,连接
,连接![]() .
.
①判断![]() 与
与![]() 面积之间的关系,并说明理由.
面积之间的关系,并说明理由.
②若![]() ,
,![]() ,
,![]() ,直接写出六边形
,直接写出六边形![]() 的面积为__________.
的面积为__________.


【答案】(1)①见解析,②8;(2)①△PQR与△PEF面积相等,理由见解析,②32.
【解析】试题分析:(1)①利用勾股定理计算后画出即;②利用恰好能覆盖△ABC的长方形的面积减去三个小直角三角形的面积即可;(2)①△PQR与△PEF面积相等,如图2,作RM⊥PQ于点M,EN⊥FP的延长线于点N,易证△PMR≌△PNE,可得RM=EN,根据等底等高的两个三角形的面积相等即可得结论;②六边形AQRDEF的面积=边长为![]() 的正方形面积+边长为
的正方形面积+边长为![]() 的正方形面积+△PEF的面积+△PQR的面积,其中两个三角形的面积分别用长方形的面积减去各个小三角形的面积.
的正方形面积+△PEF的面积+△PQR的面积,其中两个三角形的面积分别用长方形的面积减去各个小三角形的面积.
试题解析:
(![]() )①如图
)①如图![]() .
.

②![]() .
.
(![]() )①
)①![]() 与
与![]() 面积相等,
面积相等,
理由:如图![]() ,作
,作![]() 于点
于点![]() ,
,

![]() 的延长线于点
的延长线于点![]() ,
,
在![]() 与
与![]() 中,
中,
 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
![]() ,
,![]() ,
,
∴![]() .
.
②∵![]() ,
,![]() ,
,![]() ,
,
将这个六边形放入网可行中,它的面积为![]() ,
,
∴![]()
![]() .
.



科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过最高点(2,5)和点(0,4).
(1)试确定此二次函数的解析式;
(2)请你用图象法判断方程-![]() x2+x+1=0的根的情况.(画出简图)
x2+x+1=0的根的情况.(画出简图)
查看答案和解析>>
科目:初中数学 来源: 题型:
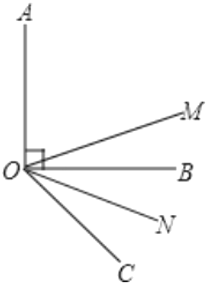
【题目】如图,已知![]() 与
与![]() 互为余角,且
互为余角,且![]() 平分
平分![]() 平分
平分![]() .
.
(1)求![]() 的度数;
的度数;
(2)如果已知![]() ,其他条件不变,则
,其他条件不变,则![]() _______度;如果已知
_______度;如果已知![]() ,其他条件不变,则
,其他条件不变,则![]() _______度;
_______度;
(3)从以上求![]() 的过程中,你得出的结论是__________.
的过程中,你得出的结论是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
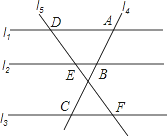
【题目】如图,直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3 , 已知EF:DF=5:8,AC=24.
(1)求AB的长;
(2)当AD=4,BE=1时,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当![]() 很大时,摸到白球的频率将会接近 .(精确到0.1)
很大时,摸到白球的频率将会接近 .(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)= .
(3)试估算盒子里黑、白两种颜色的球各有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是 ( )

A. AB=AC B. ∠ADC=∠AEB C. ∠B=∠C D. BE=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题背景)解方程:x4﹣5x2+4=0.
这是一个一元四次方程,根据该方程的特点,我们可以借助“换元法”将高次方程“降次”,进而解得未知数的值.
解:设 x2=y,那么 x4=y2,于是原方程可变为 y2﹣5y+4=0,解得 y1=1,y2=4. 当 y1=1 时,x2=1,x=±1;当 y2=4 时,x2=4,x=±2;
原方程有四个根:x1=1,x2=﹣1,x3=2,x4=﹣2.
(触类旁通)参照例题解方程:(x2+x)2﹣4(x2+x)﹣12=0;
(解决问题)已知实数 x,y 满足(2x+2y+3)(2x+2y﹣3)=27,求 x+y 的值;
(拓展迁移)分解因式:(x2+4x+3)(x2+4x+5)+1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com