
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,设购进甲种花卉x盆,全部销售后获得的利润为W元,求W与x之间的函数关系式;
(3)在(2)的条件下,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?
【答案】(1)购进甲种花卉每盆16元,乙种花卉每盆8元;(2)W=4x+100;(3)该花店共有三种购进方案,在所有的购进方案中,购买甲种花卉12盆,乙种花卉76盆时,获利最大,最大利润是148元.
【解析】试题分析:(1)根据题意可以列出相应的二元一次方程组,从而可以求得购进甲、乙两种花卉,每盆各需多少元;
(2)根据题意可以写出W与x的函数关系式;
(3)根据题意可以列出相应的不等式组,从而可以得到有几种购进方案,哪种方案获利最大,最大利润是多少.
试题解析:(1)设购进甲种花卉每盆x元,乙种花卉每盆y元,
![]() 解得,
解得, ![]()
即购进甲种花卉每盆16元,乙种花卉每盆8元;
(2)由题意可得,
W=6x+80016x8×1,
化简,得
W=4x+100,
即W与x之间的函数关系式是:W=4x+100;
(3) 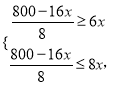
解得, ![]()
故有三种购买方案,
由W=4x+100可知,W随x的增大而增大,
故当x=12时,80016x8=76,即购买甲种花卉12盆,一种花卉76盆时,获得最大利润,此时W=4×12+100=148,
即该花店共有几三种购进方案,在所有的购进方案中,购买甲种花卉12盆,一种花卉76盆时,获利最大,最大利润是148元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】《庄子·天下》:“一尺之棰,日取其半,万世不竭.”意思是说:一尺长的木棍,每天截掉一半,永远也截不完.我国智慧的古代人在两千多年前就有了数学极限思想,今天我们运用此数学思想研究下列问题.
(规律探索)
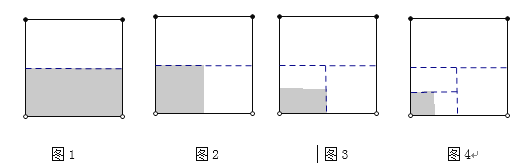
(1)如图1所示的是边长为1的正方形,将它剪掉一半,则S阴影1=1-![]() =__________;
=__________;
如图2,在图1的基础上,将阴影部分再裁剪掉—半,则S阴影2=1-![]() -(
-(![]() )2=_______;
)2=_______;
同种操作,如图3,S阴影3=1-![]() -(
-(![]() )2-(
)2-(![]() )3=__________;
)3=__________;
如图4,S阴影4=1-![]() -(
-(![]() )2-(
)2-(![]() )3-(
)3-(![]() )4=___________;
)4=___________;
……
若同种地操作n次,则S阴影n=1-![]() -(
-(![]() )2-(
)2-(![]() )3-…-(
)3-…-(![]() )n=_________.
)n=_________.
(规律归纳)
(2)直接写出![]() +
+![]() +
+![]() +…+
+…+![]() 的化简结果:_________.
的化简结果:_________.
(规律应用)
(3)直接写出算式![]() +
+![]() +
+![]() +…+
+…+![]() 的值:__________.
的值:__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
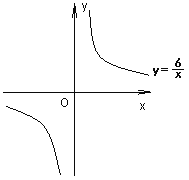
【题目】若反比例函数![]() 与一次函数
与一次函数![]() 的图象都经过点A(
的图象都经过点A(![]() ,2)
,2)
(1)求点A的坐标;
(2)求一次函数![]() 的解析式;
的解析式;
(3)设O为坐标原点,若两个函数图像的另一个交点为B,求△AOB的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019女排世界杯于9月14月至29日在日本举行,赛制为单循环比赛(即每两个队之间比赛一场),一共比赛66场,中国女排以全胜成绩卫冕世界杯冠军,为国庆70周年献上大礼,则中国队在本届世界杯比赛中连胜( )
A.10场B.11场C.12场D.13场
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)![]()
(2)(+6)-(+12)+(+9.6)-(+7.6)
(3)5×![]() ―
―![]() ×
×![]()
(4)(![]() )×(-60 )
)×(-60 )
(5)(2![]() )-(+10
)-(+10![]() )+(-8
)+(-8![]() )-(+3)
)-(+3)
(6)﹣14﹣(1﹣0.5)×![]() ×[1﹣(﹣2)2];
×[1﹣(﹣2)2];
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点B,抛物线
轴交于点B,抛物线![]() 经过原点和点C(4,0),顶点D在直线AB上。
经过原点和点C(4,0),顶点D在直线AB上。
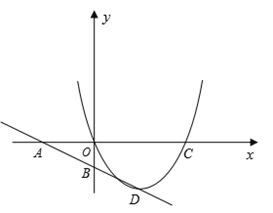
(1)求这个抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使得以P、C、D为顶点的三角形与△ACD相似。若存在,请求出点P的坐标;若不存在,请说明理由;
(3)点Q是![]() 轴上方的抛物线上的一个动点,若
轴上方的抛物线上的一个动点,若![]() ,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是( )
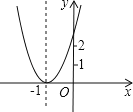
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC中,AB=AC,点D,E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.

(1)求证:∠ABE=∠ACD;
(2)求证:过点A、F的直线垂直平分线段BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BC是直径,⊙O的切线PA交CB的延长线于点P,OE∥AC交AB于点F,交PA于点E,连接BE.
(1)判断BE与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,BE=3,求AB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com