
| A. | $\left\{{\begin{array}{l}{x=-3}\\{y=13}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x=12}\\{y=-2}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x=2}\\{y=5}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x=4}\\{y=6}\end{array}}\right.$ |
科目:初中数学 来源: 题型:选择题
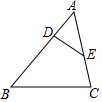 如图,△ABC中,D、E分别在AB、AC上,下列条件中不能判断△ADE∽△ACB的是( )
如图,△ABC中,D、E分别在AB、AC上,下列条件中不能判断△ADE∽△ACB的是( )| A. | ∠ADE=∠C | B. | ∠AED=∠B | C. | $\frac{AD}{AC}=\frac{AE}{AB}$ | D. | $\frac{AD}{AC}=\frac{DE}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 重量x(kg) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| 长度y(cm) | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 | 8.0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
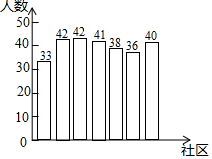 小楠所在社会实践活动小组的同学们响应“垃圾分类,从我做起”的号召,主动到附近的7个社区宣传垃圾分类.她们记录的各社区参加活动的人数如图所示,那么这组数据的众数和中位数分别是( )
小楠所在社会实践活动小组的同学们响应“垃圾分类,从我做起”的号召,主动到附近的7个社区宣传垃圾分类.她们记录的各社区参加活动的人数如图所示,那么这组数据的众数和中位数分别是( )| A. | 42,40 | B. | 42,38 | C. | 2,40 | D. | 2,38 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com