练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．已知反比例函数y=$\frac{8}{x}$，若x≥-2，则函数y的取值范围是y≤-4或y＞0．

    分析 先求出x=-2时y的值，根据函数的图象函数性质得出即可．

    解答 解：把x=-2代入y=$\frac{8}{x}$得：y=-4，
    ∵8＞0，
    ∴在每个象限内，y随x的增大而减小，图象在第一、三象限，
    ∴当x≥-2时，函数y的取值范围是y≤-4或y＞0，
    故答案为：y≤-4或y＞0．

    点评 本题考查了反比例函数的图象和性质，能熟记反比例函数的性质是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．化简：$\frac{ab+c}{a+b}$+$\frac{{a}^{2}-c}{a+b}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

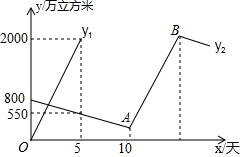    9．因南方旱情严重，乙水库的蓄水量以每天相同的速度持续减少，为缓解旱情，北方甲水库立即以管道运输的方式给予支援，如图是乙水库的蓄水量y1（单位：万立方米）关于时间x（单位：天）的函数图象和甲水库输水量y1（单位：万立方米）关于时间x（0≤x≤5）的函数图象，在单位时间内、甲水库的放水量与乙水库的进水量相同（水在排放、接收以及输送过程中的损耗不计），通过分析图象解答下列问题：
    （1）求甲水库输水量y1关于时间x（0≤x≤5）的函数解析式；
    （2）在第几天时甲水库输出的水开始注入乙水库？此时乙水库的蓄水量为多少万立方米？
    （3）求乙水库蓄水量（线段AB）的函数解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

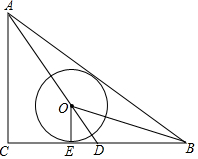    6．如图，△ABC中，∠C=90°，AC=3，AB=5，点O在BC边的中线AD上，⊙O与BC相切于点E，且∠OBA=∠OBC．
    （1）求证：AB为⊙O的切线；
    （2）求⊙O的半径；
    （3）求tan∠BAD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．圆锥的轴截面是一个边长为6cm的等边三角形，则这个圆锥的侧面积是18πcm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．先化简（$\frac{1}{x+1}+\frac{1}{x-1}$）$÷\frac{1}{{x}^{2}-1}$，然后从$\sqrt{2}$，1，-1中选取一个你认为合适的数作为x的值代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．（1）化简：$\frac{2x-6}{x-2}$÷（$\frac{5}{x-2}$-x-2）；
    （2）解一元二次方程：x2-1=2（x+1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

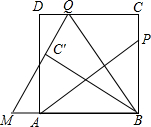    7．如图，P为正方形ABCD的边BC上一点，连接AP，过点B作BQ⊥AP，交CD于点Q，将△BQC沿BQ所在的直线对折得到△BQC′，延长QC′，交BA的延长线于点M，当AB=3，BP=2PC时，QM=$\frac{13}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．平面直角坐标系中，点P（-2，3）与点Q（a，b）关于原点对称，则a+b=-1．

    查看答案和解析>>

    同步练习册答案