
【题目】已知:抛物线y=x2﹣2(m﹣1)x﹣1﹣m
(1)当m=2时,求该抛物线的对称轴和顶点坐标;
(2)设该抛物线与x轴交于A(x1,0)、B(x2,0),x1<0<x2,与y轴交于点C,且满足![]() ,求这个抛物线的解析式;
,求这个抛物线的解析式;
(3)在(2)的条件下,是否存在着直线y=kx+b与抛物线交于点P、Q,使y轴平分△CPQ的面积?若存在,求出k,b应满足的条件;若不存在,请说明理由.
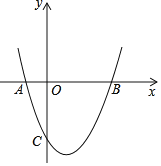
【答案】(1)对称轴直线为x=1,顶点坐标为(1,﹣4);(2)y=x2﹣2x﹣3;(3)存在,当k=﹣2且b>﹣3时直线y=kx+b与抛物线交于点P,Q使y轴平分△CPQ的面积.
【解析】
(1)将m=2代入抛物线解析式中,并且配方得出y=x2﹣2x﹣3=(x﹣1)2﹣4,即可得出结论;
(2)先表示出AO=﹣x1,OB=x2,CO=m+1>0,再用 ![]() ,建立方程化简得出(m+1)(x1+x2)=﹣2x1x2,再根据根与系数的关系得出x1+x2=2(m﹣1),x1x2=﹣(1+m),即可得出结论;
,建立方程化简得出(m+1)(x1+x2)=﹣2x1x2,再根据根与系数的关系得出x1+x2=2(m﹣1),x1x2=﹣(1+m),即可得出结论;
(3)设点P的横坐标为xP,点Q的横坐标为xQ,直线与y轴交于点E,利用面积相等得出|xP|=|xQ|,即xP=﹣xQ,再由![]() ,得出x2﹣(k+2)x﹣(b+3)=0,进而得出xP+xQ=k+2=0,即可得出结论.
,得出x2﹣(k+2)x﹣(b+3)=0,进而得出xP+xQ=k+2=0,即可得出结论.
(1)当m=2时,得出y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的对称轴直线为x=1,顶点坐标为(1,﹣4);
(2)∵x1<0<x2,
∴AO=﹣x1,OB=x2,
又∵a=1>0,
∴CO=m+1>0,
∴m>﹣1,
∵![]() ,
,
∴CO(OB﹣AO)=2AOOB,
即(m+1)(x1+x2)=﹣2x1x2
对于抛物线y=x2﹣2(m﹣1)x﹣1﹣m,
令y=0,则0=x2﹣2(m﹣1)x﹣1﹣m,
∵x1+x2=2(m﹣1),x1x2=﹣(1+m),
∴(m+1)2(m﹣1)=2(1+m),
解得m=﹣1(舍去),m=2.
∴二次函数的解析式为y=x2﹣2x﹣3.
(3)存在着直线y=kx+b与抛物线交于点P、Q,使y轴平分△CPQ的面积,
设点P的横坐标为xP,点Q的横坐标为xQ,直线与y轴交于点E,
∵S△PCE=S△QCE,![]() CE|xP|=
CE|xP|=![]() CE|xQ|,
CE|xQ|,
∴|xP|=|xQ|,
∵y轴平分△CPQ的面积,
∴点P、Q在y轴异侧,
即xP=﹣xQ,
由
得x2﹣(k+2)x﹣(b+3)=0
而xP,xQ为x2﹣(k+2)x﹣(b+3)=0的两根,
∴xP+xQ=k+2=0,
∴k=﹣2,
又∵直线与抛物线有两个交点,
∴b+3>0,即b>﹣3,
∴当k=﹣2且b>﹣3时直线y=kx+b与抛物线交于点P,Q使y轴平分△CPQ的面积.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b的图象与x轴、y轴分别交于A,B两点,与反比例函数y=![]() 的图象分别交于C,D两点,点C(2,4),点B是线段AC的中点.
的图象分别交于C,D两点,点C(2,4),点B是线段AC的中点.
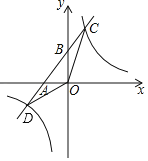
(1)求一次函数y=k1x+b与反比例函数y=![]() 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出当x取什么值时,k1x+b<![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
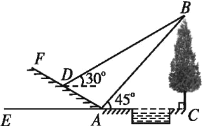
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是45°,若坡角∠FAE=30°,求大树的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有且仅有一组对角相等的凸四边形叫做“准平行四边形”.例如:凸四边形![]() 中,若
中,若![]() ,则称四边形
,则称四边形![]() 为准平行四边形.
为准平行四边形.
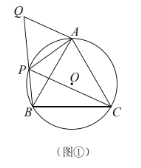
(1)如图①,![]() 是
是![]() 上的四个点,
上的四个点,![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() .求证:四边形
.求证:四边形![]() 是准平行四边形;
是准平行四边形;
(2)如图②,准平行四边形![]() 内接于
内接于![]() ,
,![]() ,若
,若![]() 的半径为
的半径为![]() ,求
,求![]() 的长;
的长;

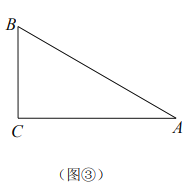
(3)如图③,在![]() 中,
中,![]() ,若四边形
,若四边形![]() 是准平行四边形,且
是准平行四边形,且![]() ,请直接写出
,请直接写出![]() 长的最大值.
长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=ax2+bx+![]() (a>0,b<0)的图象与x轴只有一个公共点A.
(a>0,b<0)的图象与x轴只有一个公共点A.
(1)当a=![]() 时,求点A的坐标;
时,求点A的坐标;
(2)求A点的坐标(只含b的代数式来表示);
(3)过点A的直线y=x+k与二次函数的图象相交于另一点B,当b≥﹣1时,求点B的横坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
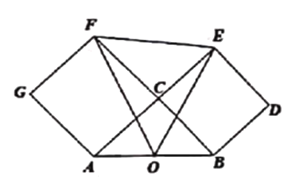
【题目】我们知道,勾股定理反映了直角三角形三条边的关系: a2+b2=c2, 而a2, b2, c2又可以看成是以a,b, c为边长的正方形的面积.如图,在Rt△ABC中,∠ACB=90°,BC=a, AC=b,O为AB的中点.分别以AC,BC 为边向△ABC外作正方形ACFG,BCED,连结OF, EF, OE,则△OEF的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
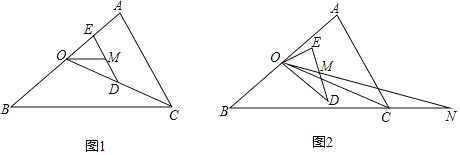
【题目】如图,OC是△ABC中AB边的中线,∠ABC=36°,点D为OC上一点,如果OD=kOC,过D作DE∥CA交于BA点E,点M是DE的中点,将△ODE绕点O顺时针旋转α度(其中0°<α<180°)后,射线OM交直线BC于点N.
(1)如果△ABC的面积为26,求△ODE的面积(用k的代数式表示);
(2)当N和B不重合时,请探究∠ONB的度数y与旋转角α的度数之间的函数关系式;
(3)写出当△ONB为等腰三角形时,旋转角α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
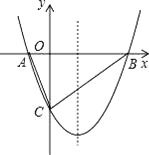
【题目】如图,抛物线y=ax2﹣![]() x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C(0,﹣2),已知B点坐标为(4,0).
x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C(0,﹣2),已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)若点M是线段BC下方的抛物线上一点,记点M到线段BC的距离为d,当d取最大值时,求出此时M点的坐标;
(3)若点P是抛物线上一点,点E是直线y=﹣x上的动点,是否存在点P、E,使以点A,点B,点P,点E为顶点的四边形是平行四边形?若存在,请直接写出点E坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com