
| A. | 6ab-b=6a | B. | $\frac{1}{a}$+$\frac{1}{b}$=$\frac{2}{a+b}$ | C. | a8÷a2=a4 | D. | (a2b)3=a6b3 |
 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:填空题
 如图,△A1OB1是边长为1的等边三角形,将其以原点O为中心在原点两侧进行位似变换,得△A2OB2,二者的位似比为1:2,将△A2OB2以x轴为对称轴进行轴对称变换,得△A3OB2再原点O为中心在原点两侧进行位似变换,得△A4OB3,二者的位似比为1:2,按此规律.则点A2016的坐标为($\frac{1}{2}$×4504,$\frac{\sqrt{3}}{2}$×4504).
如图,△A1OB1是边长为1的等边三角形,将其以原点O为中心在原点两侧进行位似变换,得△A2OB2,二者的位似比为1:2,将△A2OB2以x轴为对称轴进行轴对称变换,得△A3OB2再原点O为中心在原点两侧进行位似变换,得△A4OB3,二者的位似比为1:2,按此规律.则点A2016的坐标为($\frac{1}{2}$×4504,$\frac{\sqrt{3}}{2}$×4504).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知一次函数y=kx+b的图象如图所示,下列说法中不正确的是( )
已知一次函数y=kx+b的图象如图所示,下列说法中不正确的是( )| A. | 函数值y随x的增大而减少 | B. | kb<0 | ||
| C. | 当x<1时,y>0 | D. | k+b<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一辆动车从重庆开往成都,一辆高铁从成都开往重庆,两车同时出发,设动车离重庆的距离为y1(cm),高铁离重庆的距离为y2(km),动车行驶时间为t(h),变量y1,y2与t之间的关系图象如图所示:
一辆动车从重庆开往成都,一辆高铁从成都开往重庆,两车同时出发,设动车离重庆的距离为y1(cm),高铁离重庆的距离为y2(km),动车行驶时间为t(h),变量y1,y2与t之间的关系图象如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
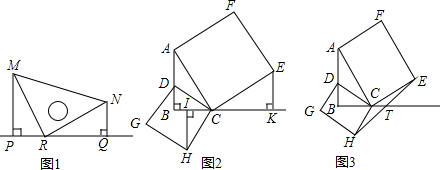
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
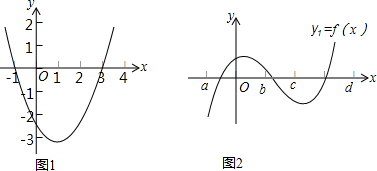
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
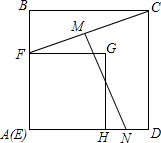 如图,面积为9cm2的正方形EFGH在面积为25cm2的正方形ABCD所在平面上移动,始终保持EF∥AB,记线段CF的中点为M,DH的中点为N,则线段MN的长度是( )
如图,面积为9cm2的正方形EFGH在面积为25cm2的正方形ABCD所在平面上移动,始终保持EF∥AB,记线段CF的中点为M,DH的中点为N,则线段MN的长度是( )| A. | $\frac{25}{4}$cm | B. | $\frac{73}{4}$cm | C. | $\frac{\sqrt{73}}{2}$cm | D. | $\frac{\sqrt{75}}{2}$cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com