
【题目】如图:A、P、B、C是⊙O上的四个点,且∠APC=∠CPB=60°
(1)判定△ABC的形状,证明你的结论;
(2)若⊙O的半径为2,求AB的长.

科目:初中数学 来源: 题型:
【题目】阅读下列材料,回答问题.
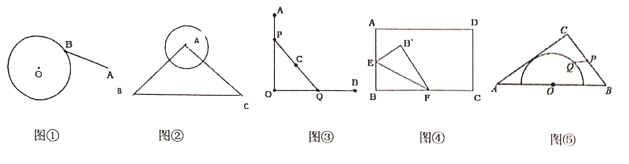
材料:求圆外一定点到圆上距离最小值是安徽省中考数学较为常见的一种题型,此类题型试题有时出题者将圆隐藏,故又称为“隐圆问题”.解决这类问题,关键是要找到动点的运动轨迹,即该动点是绕哪一个定点旋转,且能保持旋转半径不变.从而找到动点所在的隐藏圆,进面转换成圆外一点到圆心的距离减半径,求得最小值.
解决问题:
(1)如图①,圆O的半径为1,圆外一点A到圆心的距离为3,圆上一动点B,当A、O、B满足条件____________时,![]() 有最小值为____________.
有最小值为____________.
(2)如图②,等腰![]() 两腰长为5,底边长为6,以A为圆心,2为半径作圆,圆上动点P到
两腰长为5,底边长为6,以A为圆心,2为半径作圆,圆上动点P到![]() 的距离最小值为__________.
的距离最小值为__________.
(3)如图③,![]() ,P、Q分别是射线
,P、Q分别是射线![]() 、
、![]() 上两个动点,C是线段
上两个动点,C是线段![]() 的中点,且
的中点,且![]() ,则在线段
,则在线段![]() 滑动的过程中,求点C运动形成的路径长,并说明理由.
滑动的过程中,求点C运动形成的路径长,并说明理由.
(4)如图④,在矩形![]() 中,
中,![]() ,
,![]() ,点E是
,点E是![]() 中点,点F是
中点,点F是![]() 上一点,把
上一点,把![]() 沿着
沿着![]() 翻折,点B落在点
翻折,点B落在点![]() 处,求
处,求![]() 的最小值,并说明理由.
的最小值,并说明理由.
(5)如图⑤,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以边
,以边![]() 中点O为圆心,作半圆与
中点O为圆心,作半圆与![]() 相切,点P,Q分别是边
相切,点P,Q分别是边![]() 和半圆上的动点,连接
和半圆上的动点,连接![]() ,求
,求![]() 长的最小值,并说明理由.
长的最小值,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
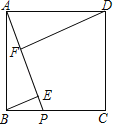
【题目】已知:如图,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E、F.
(1)求证:EF=AE﹣BE;
(2)联结BF,如课![]() =
=![]() .求证:EF=EP.
.求证:EF=EP.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=72°,将△ABC绕点B按逆时针方向旋转得到△BDE(点D与点 A是对应点,点E与点C是对应点),且边DE恰好经过点C,则∠ABD的度数为
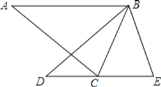
A. 36° B. 40° C. 45° D. 50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20米,如果水位上升3米,则水面CD的宽是10米.
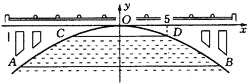
(1)建立如图所示的直角坐标系,求此抛物线的解析式;
(2)当水位在正常水位时,有一艘宽为6米的货船经过这里,船舱上有高出水面3.6米的长方体货物(货物与货船同宽).问:此船能否顺利通过这座拱桥?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点.已知FG=2,则线段AE的长度为_____.
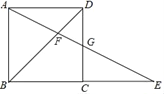
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数的图象与反比例函数的图象交于A(﹣2,1),B(1,n)两点.

根据以往所学的函数知识以及本题的条件,你能提出求解什么问题?并解决这些问题(至少三个问题).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,以BC为弦的⊙O分别与AB,AC交于点D和E,点F是BC延长线上一点,CF=AE,连接EF.

(1)如图1,BC为直径,求证:EF是⊙O的切线;
(2)如图2,EF与⊙O交于点G,⊙O的半径为1,BC的长为![]() π,求BF的长.
π,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com