
【题目】已知:如图,在平面直角坐标系中,一次函数![]()
![]() 的图象与反比例函数
的图象与反比例函数![]()
![]() 的图象交于一、三象限内的
的图象交于一、三象限内的![]() ,
,![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
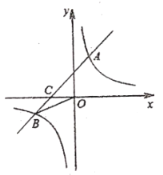
(1)求该反比例函数和一次函数的解析式;
(2)直接写出关于![]() 的不等式
的不等式![]() 的解集;
的解集;
(3)连接![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;y=x+3;(2)x<-5或0<x<2;(3)
;y=x+3;(2)x<-5或0<x<2;(3)![]()
【解析】
(1)先根据解直角三角形求得点B的坐标,利用点B的坐标求得反比例函数解析式,然后求得A点坐标,再利用A、B两点的坐标求得一次函数解析式,;
(2)根据函数图象进行观察,写出一次函数图象在反比例函数图象下方时所有点的横坐标的集合即可;
(3)求出直线AB与y轴的交点坐标,然后利用三角形面积公式求得△AOB的面积;
解:过点B作BM⊥x轴
由![]() ,
,![]()
∴![]() ,即
,即![]() ,解得:OM=5
,解得:OM=5
∴B(-5,-2)
将B(-5,-2)代入![]() 中,k=10
中,k=10
∴反比例函数的解析式为:![]()
将A![]() 代入
代入![]() 中,m=5
中,m=5
∴A(2,5)
把A(2,5)和B(-5,-2)代入![]() 中
中
![]() ,解得
,解得![]()
∴一次函数的解析式为:y=x+3;
(2)由图像可知,当x<-5或0<x<2时,一次函数值小于反比例函数值
∴不等式![]() 的解集为:x<-5或0<x<2;
的解集为:x<-5或0<x<2;
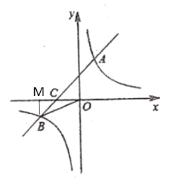
(3)连接OA,直线AB与y轴交于点E
在y=x+3中,当x=0时,y=3
∴OE=3
∴![]() .
.
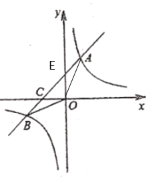


科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,与反比例函数
两点,与反比例函数![]() 交于点
交于点![]() 点
点![]() 的坐标为
的坐标为![]() 轴于点
轴于点![]() .
.

(1)点![]() 的坐标为 ;
的坐标为 ;
(2)若点![]() 为
为![]() 的中点,求反比例函数
的中点,求反比例函数![]() 的解析式;
的解析式;
(3)在(2)条件下,以![]() 为边向右作正方形
为边向右作正方形![]() 交
交![]() 于点
于点![]() 直接写出
直接写出![]() 的周长与
的周长与![]() 的周长的比.
的周长的比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《函数的图象与性质》拓展学习展示:
(问题)如图1,在平面直角坐标系中,抛物线G1:![]() 与x轴相交于A(-1,0),B(3,0)两点,与y轴交于点C,则a= ,b= .
与x轴相交于A(-1,0),B(3,0)两点,与y轴交于点C,则a= ,b= .
(操作)将图1中抛物线G1沿BC方向平移BC长度的距离得到抛物线G2,G2在y轴左侧的部分与G1在y轴右侧的部分组成的新图象记为G,如图②.请直接写出图象G对应的函数解析式.
(探究)在图2中,过点C作直线l平行于x轴,与图象G交于D,E两点.求图象G在直线l上方的部分对应的函数y随x的增大而增大时x的取值范围.
(应用)P是抛物线G2对称轴上一个动点,当△PDE是直角三角形时,直接写出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
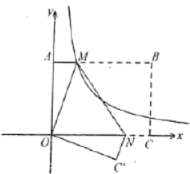
【题目】如图,在平面直角坐标系中,![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴正半轴上的点,以
轴正半轴上的点,以![]() 、
、![]() 为边,在一象限内作矩形
为边,在一象限内作矩形![]() ,且
,且![]() .将矩形
.将矩形![]() 翻折,使点
翻折,使点![]() 与原点重合,折痕为
与原点重合,折痕为![]() ,点
,点![]() 的对应点
的对应点![]() 落在第四象限,过
落在第四象限,过![]() 点的反比例函数
点的反比例函数![]()
![]() ,其图象恰好过
,其图象恰好过![]() 的中点,则点的
的中点,则点的![]() 坐标为________.
坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着智能手机的普及率越来越高以及移动支付的快捷高效性,中国移动支付在世界处于领先水平.为了解人们平时最喜欢用哪种移动支付方式,因此在某步行街对行人进行随机抽样调查,以下是根据调查结果分别整理的不完整的统计表和统计图.
移动支付方式 | 支付宝 | 微信 | 其他 |
人数/人 |
| 200 | 75 |
请你根据上述统计表和统计图提供的信息.完成下列问题:
(1)在此次调查中,使用支付宝支付的人数;
(2)求表示微信支付的扇形所对的圆心角度数;
(3)某天该步行街人流量为10万人,其中30%的人购物并选择移动支付,请你依据此次调查获得的信息估计一下当天使用微信支付的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象与直线
的图象与直线![]() 都经过点
都经过点![]() .
.
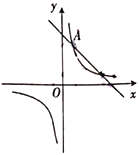
(1)求反比例函数和直线的解析式.
(2)将一次函数![]() 的图象沿
的图象沿![]() 轴向下平移
轴向下平移![]() 个单位长度,使平移后的图象与反比例函数
个单位长度,使平移后的图象与反比例函数![]() 的图象有且只有一个交点,求
的图象有且只有一个交点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB:BC=3:4,点E是对角线BD上一动点(不与点B,D重合),将矩形沿过点E的直线MN折叠,使得点A,B的对应点G,F分别在直线AD与BC上,当△DEF为直角三角形时,CN:BN的值为_____.
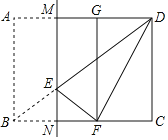
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com