
分析 ①由抛物线y=ax2+bx+c(a≠0)经过点(-1,0),得到a-b+c=0,故①正确;②由抛物线y=ax2+bx+c(a≠0)经过点(1,1),于是得到a+b+c=1,由于a-b+c=0,得到a+c=12,b=12.推出b2-4ac=14-4a(12-a)=14-2a+4a2=(2a-12)2≥0,于是得到故②错误;③当a<0时,由b2-4ac=(2a-12)2>0,得到抛物线y=ax2+bx+c与x轴有两个交点,设另一个交点的横坐标为x,根据根浴系数的关系得到x=1-$\frac{1}{2a}$>1,即抛物线与x轴必有一个交点在点(1,0)的右侧,故③正确;④抛物线的对称轴公式即可得到x=-$\frac{b}{2a}$=-$\frac{\frac{1}{2}}{2a}$=-$\frac{1}{4a}$,故④正确.
解答 解:①∵抛物线y=ax2+bx+c(a≠0)经过点(-1,0),∴a-b+c=0,故①正确;
②∵抛物线y=ax2+bx+c(a≠0)经过点(1,1),∴a+b+c=1,又a-b+c=0,
两式相加,得2(a+c)=1,a+c=12,
两式相减,得2b=1,b=12.
∵b2-4ac=14-4a(12-a)=14-2a+4a2=(2a-12)2,
当2a-12=0,即a=14时,b2-4ac=0,故②错误;
③当a<0时,∵b2-4ac=(2a-12)2>0,
∴抛物线y=ax2+bx+c与x轴有两个交点,设另一个交点的横坐标为x,
则-1•x=$\frac{c}{a}$=$\frac{\frac{1}{2}-a}{a}$=$\frac{1}{2a}$-1,即x=1-$\frac{1}{2a}$,
∵a<0,∴-$\frac{1}{2a}$>0,
∴x=1-$\frac{1}{2a}$>1,
即抛物线与x轴必有一个交点在点(1,0)的右侧,故③正确;
④抛物线的对称轴为x=-$\frac{b}{2a}$=-$\frac{\frac{1}{2}}{2a}$=-$\frac{1}{4a}$,故④正确.
故答案为:①③④.
点评 本题考查了二次函数的图象与系数的关系熟练掌握y=ax2+bx+c系数符号的确定:(1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0.(2)b由对称轴和a的符号确定:由对称轴公式x=$\frac{b}{2a}$判断符号.(3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0.(4)b2-4ac由抛物线与x轴交点的个数确定:2个交点,b2-4ac>0;1个交点,b2-4ac=0;没有交点,b2-4ac<0,是解题的关键.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:选择题
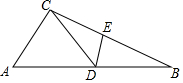 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=60°,则∠CDE的度数为( )
如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=60°,则∠CDE的度数为( )| A. | 45° | B. | 50° | C. | 51° | D. | 52° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当m=-2时,函数图象与x轴没有交点 | |
| B. | 当m=1时,函数图象过点(-1,1) | |
| C. | 若m<0,则当x≤1时,y随x的增大而增大 | |
| D. | 若m>0,则当x≥1时,y随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD、OD.
如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD、OD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 905×1010 | B. | 90.5×1011 | C. | 9.05×1012 | D. | 0.95×1013 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com