
 x2+x+6经过B,C两点,
x2+x+6经过B,C两点,
 x2+x+6经过B,C两点,
x2+x+6经过B,C两点, 对称,
对称, ,
, =
= ,∴
,∴ =
= =
= ,
, ,解得
,解得 ,
, x+5,
x+5,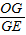 =
= =
= =
= ,
,
 =
=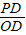 =
=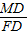 ,
, =
= =5
=5 ,
, =
=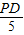 =
= ,∴MP=2
,∴MP=2 ,PD=
,PD= ,
, ,5+
,5+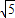 ),N(-2
),N(-2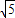 ,
, );
);
 x+5上,∴设M(a,-
x+5上,∴设M(a,- a+5),
a+5), a+5)2=52,
a+5)2=52, ,∴-
,∴- xM+5=
xM+5= ,xM=5,
,xM=5,
 ).
). ,
, ),N2(4,8),N3(-5,
),N2(4,8),N3(-5, ).
).

 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
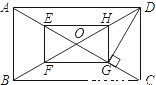
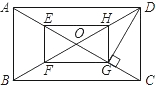 如图,O是矩形ABCD的对角线的交点,E、F、G、H分别是OA、OB、OC、OD上的点,且AE=BF=CG=DH.
如图,O是矩形ABCD的对角线的交点,E、F、G、H分别是OA、OB、OC、OD上的点,且AE=BF=CG=DH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,O是矩形ABCD的对角线的交点,E、F、G、H分别是OA、OB、OC、OD上的点,且AE=BF=CG=DH.
如图,O是矩形ABCD的对角线的交点,E、F、G、H分别是OA、OB、OC、OD上的点,且AE=BF=CG=DH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
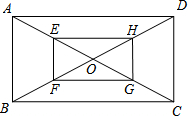 如图,O是矩形ABCD的对角线的交点,E、F、G、H分别是OA、OB、OC、OD上的点,且AE=BF=CG=DH.
如图,O是矩形ABCD的对角线的交点,E、F、G、H分别是OA、OB、OC、OD上的点,且AE=BF=CG=DH.查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《四边形》(10)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年广西崇左市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com