
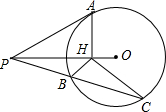
 如图,已知PA切⊙O于A,∠APO=30°,AH⊥PO于H,任作割线PBC交⊙O于点B、C,计算
如图,已知PA切⊙O于A,∠APO=30°,AH⊥PO于H,任作割线PBC交⊙O于点B、C,计算| HC-HB |
| BC |
| BH |
| OC |
| PB |
| PO |
| BH |
| PB |
| OC |
| PO |
| OB |
| HC |
| PO |
| PC |
| OB |
| PO |
| HC |
| PC |
| BH |
| PB |
| HC |
| PC |
| HC |
| BH |
| PC |
| PB |
| HC-BH |
| BH |
| PC-PB |
| PB |
| BC |
| PB |
| HC-HB |
| BC |
| BH |
| PB |
| HC-HB |
| BC |
| OC |
| PO |
| OA |
| OP |
| HC-HB |
| BC |

| BH |
| OC |
| PB |
| PO |
| BH |
| PB |
| OC |
| PO |
| OB |
| HC |
| PO |
| PC |
| OB |
| PO |
| HC |
| PC |
| BH |
| PB |
| HC |
| PC |
| HC |
| BH |
| PC |
| PB |
| HC-BH |
| BH |
| PC-PB |
| PB |
| BC |
| PB |
| HC-HB |
| BC |
| BH |
| PB |
| HC-HB |
| BC |
| OC |
| PO |
| OA |
| OP |
| HC-HB |
| BC |
| 1 |
| 2 |


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
 在△ABC中,已知,DE∥BC,则S△ADE:S梯形BCED=1:8.
在△ABC中,已知,DE∥BC,则S△ADE:S梯形BCED=1:8.查看答案和解析>>
科目:初中数学 来源: 题型:
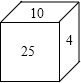 如图,有一个正方体木块,每个面上写了一个自然数,并且相对的两个面上的数字之和都相等.现在只能看到三个面上写的数字,如果看不见的三个面上写的都是质数,那么这三个质数是?
如图,有一个正方体木块,每个面上写了一个自然数,并且相对的两个面上的数字之和都相等.现在只能看到三个面上写的数字,如果看不见的三个面上写的都是质数,那么这三个质数是?查看答案和解析>>
科目:初中数学 来源: 题型:
| A、100m2 |
| B、1000m2 |
| C、10000m2 |
| D、100000m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 为了预防流感,某中学在周末用药熏消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物释放完毕后y与x成反比例;整个过程中y与x的图象如右图,据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放完毕开始至少需经过( )小时,学生才能进入教室.
为了预防流感,某中学在周末用药熏消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物释放完毕后y与x成反比例;整个过程中y与x的图象如右图,据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放完毕开始至少需经过( )小时,学生才能进入教室.| A、4.2 | B、4 |
| C、3.8 | D、3.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com