
【题目】如图,已知抛物线y=﹣x2﹣2x+m+1与x轴交于A(x1 , 0)、B(x2 , 0)两点,且x1<0,x2>0,与y轴交于点C,顶点为P.(提示:若x1 , x2是一元二次方程ax2+bx+c=0(a≠0)的两个实根,则x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() )
)
(1)求m的取值范围;
(2)若OA=3OB,求抛物线的解析式;
(3)在(2)中抛物线的对称轴PD上,存在点Q使得△BQC的周长最短,试求出点Q的坐标.
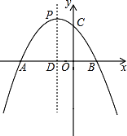
【答案】(1)m>﹣1;(2)y=﹣x2﹣2x+3;(3)存在点Q(﹣1,2)使得△BQC的周长最短.
【解析】
(1)将抛物线的问题转化到一元二次方程中,利用一元二次方程根的判别式和根与系数的关系解决;
(2)先用一元二次方程的两根表示出OA,OB,再用根与系数的关系即可;
(3)先由于点A,B关于抛物线的对称轴PD对称,连接AC与PD的交点就是使△BQC的周长最短,然后确定出直线AC解析式,最后将抛物线的对称轴代入直线AC解析式中即可.
(1)令y=0,则有﹣x2﹣2x+m+1=0,
即:x1 , x2是一元二次方程x2+2x﹣(m+1)=0,
∵抛物线y=﹣x2﹣2x+m+1与x轴交于A(x1 , 0)、B(x2 , 0)两点,
∴x1x2=﹣(m+1),x1+x2=﹣2,
△=4+4(m+1)>0,
∴m>﹣2
∵x1<0,x2>0,
∴x1x2<0,
∴﹣(m+1)<0,
∴m>﹣1,
即m>﹣1
(2)解:∵A(x1 , 0)、B(x2 , 0)两点,且x1<0,x2>0,
∴OA=﹣x1 , OB=x2 ,
∵OA=3OB,
∴﹣x1=3x2 , ①
由(1)知,x1+x2=﹣2,②
x1x2=﹣(m+1),③
联立①②③得,x1=﹣3,x2=1,m=2,
∴抛物线的解析式y=﹣x2﹣2x+3
(3)存在点Q,
理由:如图,
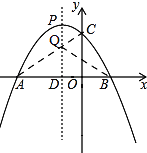
连接AC交PD于Q,点Q就是使得△BQC的周长最短,(∵点A,B关于抛物线的对称轴PD对称,)
连接BQ,
由(2)知,抛物线的解析式y=﹣x2﹣2x+3;x1=﹣3,
∴抛物线的对称轴PD为x=﹣1,C(0,3),A(﹣3,0),
∴用待定系数法得出,直线AC解析式为y=x+3,
当x=﹣1时,y=2,
∴Q(﹣1,2),
∴点Q(﹣1,2)使得△BQC的周长最短


科目:初中数学 来源: 题型:
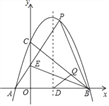
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C(0,4).
(1)求此抛物线的解析式;
(2)设点P(2,n)在此抛物线上,AP交y轴于点E,连接BE,BP,请判断△BEP的形状,并说明理由;
(3)设抛物线的对称轴交x轴于点D,在线段BC上是否存在点Q,使得△DBQ成为等腰直角三角形?若存在,求出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
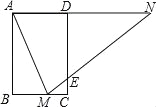
【题目】如图,矩形ABCD中,AB=3,BC=2,点M在BC上,连接AM,作∠AMN=∠AMB,点N在直线AD上,MN交CD于点E
(1)求证:△AMN是等腰三角形;
(2)求BMAN的最大值;
(3)当M为BC中点时,求ME的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在一次社会实践活动中,组织学生参观了虎园、烈士陵园、博物馆和植物园,为了解本次社会实践活动的效果,学校随机抽取了部分学生,对“最喜欢的景点”进行了问卷调查,并根据统计结果绘制了如下不完整的统计图.其中最喜欢烈士陵园的学生人数与最喜欢博物馆的学生人数之比为2:1,请结合统计图解答下列问题:
(1)本次活动抽查了 名学生;
(2)请补全条形统计图;
(3)在扇形统计图中,最喜欢植物园的学生人数所对应扇形的圆心角是 度;
(4)该校此次参加社会实践活动的学生有720人,请求出最喜欢烈士陵园的人数约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+1与二次函数y2=ax2+bx﹣2交于A,B两点,且A(1,0)抛物线的对称轴是x=﹣![]() .
.
(1)求k和a、b的值;
(2)求不等式kx+1>ax2+bx﹣2的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
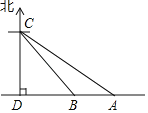
【题目】据调查,超速行驶是引发交通事故的主要原因之一.小强用所学知识对一条笔直公路上的车辆进行测速,如图所示,观测点C到公路的距离CD=200m,检测路段的起点A位于点C的南偏东60°方向上,终点B位于点C的南偏东45°方向上.一辆轿车由东向西匀速行驶,测得此车由A处行驶到B处的时间为10s.问此车是否超过了该路段16m/s的限制速度?(观测点C离地面的距离忽略不计,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
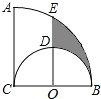
【题目】如图,![]() ,
,![]() ,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作
,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作![]() ,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是
,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是![]()
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+bx+c与x轴交于A(2,0),B(﹣4,0)两点.

(1)求该抛物线的解析式;
(2)若抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(3)在抛物线的第二象限图象上是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若不存,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
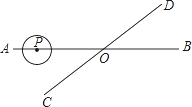
【题目】如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在直线AB上,且与点O的距离为6cm.如果⊙P以1cm∕s的速度,沿由A向B的方向移动,那么________秒种后⊙P与直线CD相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com