
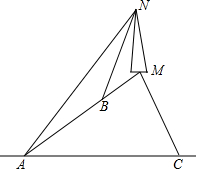
 如图所示,在小山顶上有一座信号发射塔MN,在山坡坡脚A处测得塔尖点N的仰角为45°,某人沿坡度为i=1:$\sqrt{3}$坡面上山,行走200米到B处,测得塔尖点N的仰角为60°,已知A,B,M在同一条直线上,求:
如图所示,在小山顶上有一座信号发射塔MN,在山坡坡脚A处测得塔尖点N的仰角为45°,某人沿坡度为i=1:$\sqrt{3}$坡面上山,行走200米到B处,测得塔尖点N的仰角为60°,已知A,B,M在同一条直线上,求:分析 (1)根据AB的长和坡度,利用锐角三角函数可以求得点B处的垂直高度;
(2)作出合适的辅助线,然后根据等腰三角形的性质和锐角三角函数即可求得发射塔MN的高度.
解答 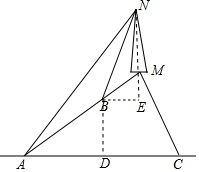 解:(1)作BD⊥AC于点D,
解:(1)作BD⊥AC于点D,
∵坡度i=1:$\sqrt{3}$,
∴tan∠BAD=$\frac{BD}{AD}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$,
∴∠BAD=30°,
∵AB=200米,
∴BD=AB•sin30°=200×$\frac{1}{2}$=100米,
答:点B处的垂直高度是100米;
(2)作BE∥AC交NM的延长线于点E,
由题意可得,
∠NAC=45°,∠NBE=60°,
∵∠BAD=30°,
∴∠NAB=15°,∠BNE=30°,∠ANE=45°,
∴∠NAB=∠ANB=15°,
∴AB=BN,
∴BN=200,
∴BE=BN•sin∠BNE=100,NE=BN•cos∠BNE=100$\sqrt{3}$,
∴ME=BE•tan∠MBE=100×$\frac{\sqrt{3}}{3}$=$\frac{100\sqrt{3}}{3}$,
∴MN=NE-ME=100$\sqrt{3}$-$\frac{100\sqrt{3}}{3}$=$\frac{200\sqrt{3}}{3}$,
答:发射塔MN的高度是$\frac{200\sqrt{3}}{3}$米.
点评 本题考查解直角三角形的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数解答.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
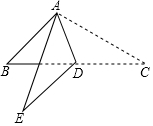 如图,△ABC中,∠B=40°,∠C=30°,点D为边BC上一点,将△ADC沿直线AD折叠后,点C落到点E处,若DE∥AB,则∠ADC的度数为110°.
如图,△ABC中,∠B=40°,∠C=30°,点D为边BC上一点,将△ADC沿直线AD折叠后,点C落到点E处,若DE∥AB,则∠ADC的度数为110°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
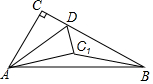 如图.在Rt△ABC中.∠ACB=90°.∠ABC=30°,AB=6.点D是BC边上一动点,连接AD.将△ACD沿AD折叠.点C落在点C1处.连接C1B.若△BDC1为直角三角形.则BD=2$\sqrt{3}$或3$\sqrt{3}$-3.
如图.在Rt△ABC中.∠ACB=90°.∠ABC=30°,AB=6.点D是BC边上一动点,连接AD.将△ACD沿AD折叠.点C落在点C1处.连接C1B.若△BDC1为直角三角形.则BD=2$\sqrt{3}$或3$\sqrt{3}$-3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
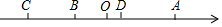 如图,在数轴上,点A表示的数是50,点C和点A到原点O距离相等,点D在点A的左侧距离A点40个单位长度,点B是线段CD的中点.
如图,在数轴上,点A表示的数是50,点C和点A到原点O距离相等,点D在点A的左侧距离A点40个单位长度,点B是线段CD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com