
 在平行四边形ABCD中,AE,CF分别平分∠BAD和∠BCD.
在平行四边形ABCD中,AE,CF分别平分∠BAD和∠BCD.分析 (1)先由平行四边形的性质可得:AD∥BC、∠BAD=∠BCD,进而可得AF∥CE,然后由AE,CF分别平分∠BAD和∠BCD,可得∠BAE=∠DAE=$\frac{1}{2}∠BAD$,∠BCF=∠DCF=$\frac{1}{2}∠BCD$,从而可得∠DAE=∠BCF,然后由AD∥BC,根据两直线平行,内错角相等,可得∠DAE=∠BEA,从而可得∠BEA=∠BCF,然后由同位角相等,两直线平行即可判断AE∥CF,然后根据两组对边分别平行的四边形是平行四边形,即可证明四边形AECF是平行四边形;
(2)①由(1)知,∠BEA=∠BAE,然后由∠B=60°,可判断△ABE是等边三角形,可得AB=BE=AE=4,然后由BE=2CE,可得CE=2,进而可求四边形AECF的周长;
②过点A作AG⊥BC,垂足为G,在等边三角形ABE中,由等边三角形的性质可求EG的值,然后由勾股定理可求AG的值,然后根据平行四边形的面积公式即可计算四边形AECF的面积.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC、∠BAD=∠BCD,
∴∠DAE=∠BEA,AF∥EC,
∵AE,CF分别平分∠BAD和∠BCD,
∴∠BAE=∠DAE=$\frac{1}{2}∠BAD$,∠BCF=∠DCF=$\frac{1}{2}∠BCD$,
∴∠DAE=∠BCF,
∴∠BEA=∠BCF,
∴AE∥CF,
∴四边形AECF是平行四边形;
(2)解:①∠BAE=∠DAE,∠DAE=∠BEA,
∴∠BEA=∠BAE,
∵∠B=60°,∠BEA+∠BAE+∠B=180°,
∴∠BEA=∠BAE=$\frac{180°-∠B}{2}$=60°,
∴△ABE是等边三角形,
∴AB=BE=AE=4,
∵BE=2CE,
∴CE=2,
∵四边形AECF是平行四边形,
∴AF=EC=2,AE=CF=4,
∴四边形AECF的周长为:AF+EC+AE+CF=12;
②过点A作AG⊥BC,垂足为G,如图所示,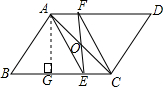
∵△ABE是等边三角形,AG⊥BE,
∴GE=$\frac{1}{2}$BE=2,
在Rt△AGE中,由勾股定理得:
AG=$\sqrt{A{E}^{2}-G{E}^{2}}$=$\sqrt{12}$=2$\sqrt{3}$,
∴S?AECF=EC•AG=2×2$\sqrt{3}$=4$\sqrt{3}$.
点评 本题考查了平行四边形的性质以及判定方法,平行四边形的周长及面积的计算,(1)证明∠AEB=∠FCB,得到AE∥CF是证明的关键;(2)证明△ABE是等边三角形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
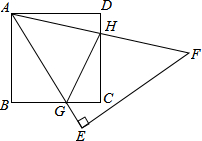 如图,已知正方形ABCD和等腰直角三角形△AEF,∠E=90°,AE和BC交于点G,AF和CD交于点H,正方形ABCD的面积为1cm2,则△CGH的周长为2.
如图,已知正方形ABCD和等腰直角三角形△AEF,∠E=90°,AE和BC交于点G,AF和CD交于点H,正方形ABCD的面积为1cm2,则△CGH的周长为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小麦与小辉在玩游戏,她们定义了一种新的规则,用象棋的“相”、“仕”、“帅”、“兵”来比较大小.共有10个棋子:2个“相”,2个“仕”,1个“帅”,5个“兵”.游戏规则如下:
小麦与小辉在玩游戏,她们定义了一种新的规则,用象棋的“相”、“仕”、“帅”、“兵”来比较大小.共有10个棋子:2个“相”,2个“仕”,1个“帅”,5个“兵”.游戏规则如下:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=9 | B. | a=5 | C. | a≤9 | D. | a≤5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com