
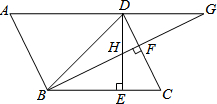
 如图,已知?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE;②∠A=∠BHE;③AB=BH;④BH=HG.
如图,已知?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE;②∠A=∠BHE;③AB=BH;④BH=HG.分析 求出BE=DE,由勾股定理得出BD2=DE2+BE2,即可判断①;求出∠DHF=∠C,根据平行四边形的性质得出AB=CD,∠A=∠C,即可判断②;证△BHE≌△DCE,推出BH=DC,根据AB=CD即可判断③;根据AB=DC=BH和已知判断④即可.
解答 解:∵DH⊥BC,
∴∠DEB=90°,
∵∠DBC=45°,
∴∠BDE=45°=∠DBE,
∴BE=DE,
由勾股定理得:BD2=DE2+BE2,
即BD=$\sqrt{2}$DE,∴①正确;
∵DE⊥BC,BF⊥CD,
∴∠DEC=∠HFD=90°,
∴∠DHF+∠EDC=90°,∠EDC+∠C=90°,
∴∠DHF=∠C,
∵四边形ABCD是平行四边形,
∴AB=CD,∠A=∠C,
∵∠DHF=∠BHE,
∴∠A=∠BHE,∴②正确;
在△BHE和△DCE中
$\left\{\begin{array}{l}{∠HBE=∠EDC}\\{BE=DE}\\{∠BEH=∠DEC}\end{array}\right.$
∴△BHE≌△DCE,
∴BH=DC,
∵AB=CD,
∴BH=AB,∴③正确;
∵根据已知不能推出BH=HG,∴④错误;
故答案为:①②③.
点评 本题考查了平行四边形的性质等腰三角形的性质,全等三角形的性质和判定,勾股定理的应用,能综合运用性质进行推理是解此题的关键,综合性比较强,有一定的难度.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,它是由6个面积为1的小正方形组成的长方形,点A、B、C、D、E、F是小正方形的顶点,以这六个点中的任意三点为顶点,组成面积是1的三角形的个数是10.
如图,它是由6个面积为1的小正方形组成的长方形,点A、B、C、D、E、F是小正方形的顶点,以这六个点中的任意三点为顶点,组成面积是1的三角形的个数是10.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
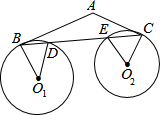 如图,AB切圆O1于B点,AC切圆O2于C点,BC分别交圆O1、圆O2于D、E两点.若∠BO1D=40°,∠CO2E=60°,则∠A的度数为何?( )
如图,AB切圆O1于B点,AC切圆O2于C点,BC分别交圆O1、圆O2于D、E两点.若∠BO1D=40°,∠CO2E=60°,则∠A的度数为何?( )| A. | 100 | B. | 120 | C. | 130 | D. | 140 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
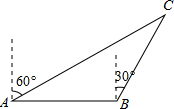 如图,海中有一灯塔C,它的周围11海里内有暗礁.一渔船以18海里/时的速度由西向东航行,在A点测得灯塔C位于北偏东60°的方向上,航行40分钟到达B点,此时测得灯塔C位于北偏东30°的方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
如图,海中有一灯塔C,它的周围11海里内有暗礁.一渔船以18海里/时的速度由西向东航行,在A点测得灯塔C位于北偏东60°的方向上,航行40分钟到达B点,此时测得灯塔C位于北偏东30°的方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com