
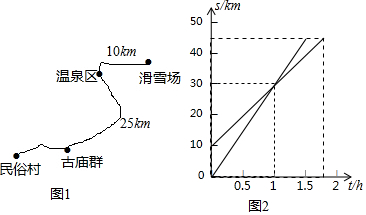
���� ��1����������ͺ���ͼ�����������״������Ⱥ֮���·�̣�
��2�����ݺ���ͼ���е����ݿ������С����С�������״�֮���·��s����ʱ��t�ĺ�������ʽ��
��3����������������С�����ﻬѩ����ʱ�䣬�Ӷ�������õ�С�����ﻬѩ��ʱ��С���뻬ѩ����·�̣�
��� �⣺��1��������ɵã�
���״������Ⱥ֮���·��Ϊ��10-0=10��km����
�ʴ�Ϊ��10��
��2����С�������״�֮���·��s����ʱ��t�ĺ�������ʽ��s=kt��
k��1=30����k=30��
��С�������״�֮���·��s����ʱ��t�ĺ�������ʽ��s=30t��
��С�������״�֮���·��s����ʱ��t�ĺ�������ʽ��s=at+b��
$\left\{\begin{array}{l}{b=10}\\{a+b=30}\end{array}\right.$����$\left\{\begin{array}{l}{a=20}\\{b=10}\end{array}\right.$��
��С�������״�֮���·��s����ʱ��t�ĺ�������ʽ��s=20t+10��
��3��������ɵã�
��s=45����s=30t����t=1.5��
��t=1.5����s=20t+10����s=40��
45-40=5��
�𣺵�С�����ﻬѩ��ʱ��С���뻬ѩ����·����5km��
���� ���⿼һ�κ�����Ӧ�ã������Ĺؼ�����ȷ���⣬�ҳ�����������Ҫ������������һ�κ��������ʺ����ν�ϵĽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 �ҹ��Ŵ���ѧ����ˬ�ġ�����Բ��ͼ�������ĸ�ȫ�ȵ�ֱ�����������м��һ��С������ƴ��һ���������Σ���ͼ��ʾ��������������ε������49��С�����ε����Ϊ4��ֱ�������ε���ֱ�DZ߳��ֱ�Ϊa��b����ô���н��ۣ�
�ҹ��Ŵ���ѧ����ˬ�ġ�����Բ��ͼ�������ĸ�ȫ�ȵ�ֱ�����������м��һ��С������ƴ��һ���������Σ���ͼ��ʾ��������������ε������49��С�����ε����Ϊ4��ֱ�������ε���ֱ�DZ߳��ֱ�Ϊa��b����ô���н��ۣ�| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
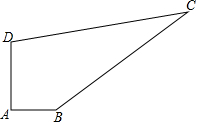 ��ͼ���ı���ABCD�У�AB=3��AD=4��BC=12��CD=13���ҡ�DAB=90�㣬������ı��ε������
��ͼ���ı���ABCD�У�AB=3��AD=4��BC=12��CD=13���ҡ�DAB=90�㣬������ı��ε�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 301 | B�� | 302 | C�� | 303 | D�� | 304 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��AB�뷴����������ͼ����A��-4��2����B��2��n�����㣮
��ͼ��ֱ��AB�뷴����������ͼ����A��-4��2����B��2��n�����㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9 | B�� | 10 | C�� | 11 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ���ı���ABCD�У�AB=$\sqrt{13}$��AD=4��������AE���ۺ�Bǡ�����C�غϣ����ۺ�AE�ij�Ϊ3��
��ͼ����ƽ���ı���ABCD�У�AB=$\sqrt{13}$��AD=4��������AE���ۺ�Bǡ�����C�غϣ����ۺ�AE�ij�Ϊ3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com