
已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.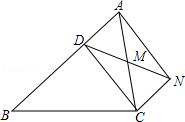
①求证:CD=AN;
②若∠AMD=2∠MCD,求证:四边形ADCN是矩形.
①先根据平行线的性质可得∠DAC=∠NCA,再有MA=MC,∠AMD=∠CMN可证得△AMD≌△CMN,即可得到AD=CN,再结合AD∥CN可得四边形ADCN是平行四边形,从而得到结论;
②∵由∠AMD=2∠MCD,∠AMD=∠MCD+∠MDC,可得∠MCD=∠MDC,即可得到MD=MC,由①知四边形ADCN是平行四边形,即可得到MD=MN=MA=MC,从而得到结论.
解析试题分析:①∵CN∥AB,
∴∠DAC=∠NCA,
在△AMD和△CMN中,
∵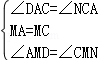 ,
,
∴△AMD≌△CMN(ASA),
∴AD=CN,
又∵AD∥CN,
∴四边形ADCN是平行四边形,
∴CD=AN;
②∵∠AMD=2∠MCD,∠AMD=∠MCD+∠MDC,
∴∠MCD=∠MDC,
∴MD=MC,
由①知四边形ADCN是平行四边形,
∴MD=MN=MA=MC,
∴AC=DN,
∴四边形ADCN是矩形.
考点:全等三角形的判定和性质,平行四边形、矩形的判定
点评:全等三角形的判定和性质及特殊四边形的判定是初中数学中极为重要的知识,贯穿于整个初中数学,再中考中极为常见,需熟练掌握.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
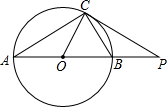 (2004•西藏)已知,如图,P是⊙O外一点,PC切⊙O于点C,割线PO交⊙O于点B、A,且AC=PC.
(2004•西藏)已知,如图,P是⊙O外一点,PC切⊙O于点C,割线PO交⊙O于点B、A,且AC=PC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com