
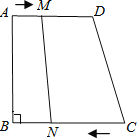
【题目】如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=15cm,BC=21cm,点M从A点开始,沿AD边向D运动,速度为1厘米/秒,点N从点C开始沿CB边向点B运动,速度为2厘米/秒,设四边形MNCD的面积为S.
(1)写出面积S与时间t之间的函数关系式;
(2)当t为何值时,四边形MNCD是平行四边形?
(3)当t为何值时,四边形MNCD是等腰梯形?
【答案】(1)S=7t+105;(2)t=5;(3)t=9
【解析】
(1)用t表示出AM、BN,然后根据梯形的面积公式求解即可求得答案;
(2)用t表示出MD、CN,然后根据平行四边形对边相等可得MD=CN,然后计算即可得解;
(3)过点D作DE⊥BC于E,然后判断出四边形ABED是矩形,根据矩形的对边相等求出BE,再求出CE,然后表示出MD,再根据等腰梯形的性质,四边形MNCD为等腰梯形时,CN=2CE+MD,列出方程求解即可.
(1)根据题意得:AM=tcm,CN=2tcm,则MD=AD﹣AM=15﹣t(cm),
∴S=![]() (MD+CN)AB=
(MD+CN)AB=![]() ×(15﹣t+2t)×14=7t+105(cm2);
×(15﹣t+2t)×14=7t+105(cm2);
∴面积S与时间t之间的函数关系式为:S=7t+105;
(2)∵点M的速度为1cm/s,点N的速度为2cm/s,
∴MD=AD﹣AM=15﹣t,CN=2t,
四边形MNCD是平行四边形时,MD=CN,
∴15﹣t=2t,
解得t=5;
∴当t=5时,四边形MNCD是平行四边形;
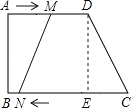
(3)如图,过点D作DE⊥BC于E,
∵AD∥BC,∠B=90°,
∴四边形ABED是矩形,
∴BE=AD=15cm,
∴CE=BC﹣BE=21﹣15=6cm,
四边形MNCD是等腰梯形时,CN=2CE+MD,
∴2t=2×6+15﹣t,
解得t=9.
∴当t=9时,四边形MNCD是等腰梯形.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】某化妆品店老板到厂家购A、B两种品牌店化妆品,若购进![]() 品牌的化妆品5套,
品牌的化妆品5套,![]() 品牌的化妆品6套,需要950元;若购进
品牌的化妆品6套,需要950元;若购进![]() 品牌的化妆品3套,
品牌的化妆品3套,![]() 品牌的化妆品2套,需要450元.
品牌的化妆品2套,需要450元.
(1)求![]() 、
、![]() 两种品牌的化妆品每套进价分别为多少元?
两种品牌的化妆品每套进价分别为多少元?
(2)若销售1套![]() 品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进
品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进![]() 品牌化妆品的数量比购进
品牌化妆品的数量比购进![]() 品牌的化妆品数量的2倍还多4套,且
品牌的化妆品数量的2倍还多4套,且![]() 品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点且AE=BF,连接CE、AF交于点H,连接DH交AG于点O,则下列结论①△ABF≌△CAE;②∠AHC=120°;③AE+CH>CD,中正确的是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一水果店,从批发市场按4元![]() 千克的价格购进10吨苹果,为了保鲜放在冷藏室里,但每天仍有一些苹果变质,平均每天有50千克变质丢弃,且每存放一天需要各种费用300元,据预测,每天每千克价格上涨
千克的价格购进10吨苹果,为了保鲜放在冷藏室里,但每天仍有一些苹果变质,平均每天有50千克变质丢弃,且每存放一天需要各种费用300元,据预测,每天每千克价格上涨![]() 元.
元.
![]() 设x天后每千克苹果的价格为p元,写出p与x的函数关系式;
设x天后每千克苹果的价格为p元,写出p与x的函数关系式;
![]() 若存放x天后将苹果一次性售出,设销售总金额为y元,求出y与x的函数关系式;
若存放x天后将苹果一次性售出,设销售总金额为y元,求出y与x的函数关系式;
![]() 该水果店将这批水果存放多少天后一次性售出,可以获得最大利润,最大利润为多少?
该水果店将这批水果存放多少天后一次性售出,可以获得最大利润,最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交
的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交![]() 轴、
轴、![]() 轴于点C、D,且S△PBD=4,
轴于点C、D,且S△PBD=4, ![]() .
.

(1)求点D的坐标;
(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当![]() 时,一次函数的值大于反比例函数的值的
时,一次函数的值大于反比例函数的值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
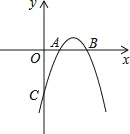
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).
(1)求抛物线的解析式和顶点坐标;
(2)将该抛物线向左平移 个单位长度后,可使平移后的抛物线的顶点落在直线y=﹣x上,并写出平移后抛物线的解析式: ;
(3)观察图象,写出关于x的不等式ax2+bx+c+3>0的解集 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com