
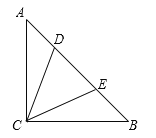
【题目】如图,在Rt△ABC中,∠ACB = 90°,![]() ,点D、E分别在边AB上,且AD = 2,∠DCE = 45°,那么DE =___________.
,点D、E分别在边AB上,且AD = 2,∠DCE = 45°,那么DE =___________.
【答案】![]()
【解析】
将△BCE绕点C逆时针旋转90°得到△ACF,连接DF,由旋转的性质可得AF=BE,CF=BC,∠FAC=∠ABC=45°=∠CAB,∠ACF=∠BCE,即可证△FCD≌△ECD,可得DE=DF,根据勾股定理可求DE的长度.
解:如图,将△BCE绕点C逆时针旋转90°得到△ACF,连接DF,
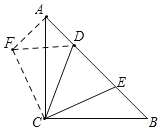
∵∠ACB=90°,AC=BC=4![]() ,
,
∴AB=8,∠CAB=∠ABC,
∵AD=2,
∴BD=6=DE+BE,
∵将△BCE绕点C逆时针旋转90°得到△ACF
∴△AFC≌△BEC
∴AF=BE,CF=BC,∠FAC=∠ABC=45°=∠CAB,∠ACF=∠BCE,
∴∠FAD=90°
∵∠DCE=45°,∠ACB=90°,
∴∠ACD+∠BCE=45°,
∴∠ACD+∠FCA=45°=∠DCE,且CF=CE,CD=CD,
∴△FCD≌△ECD(SAS)
∴DE=DF,
在Rt△ADF中,DF2=AD2+AF2,
∴DE2=4+(6﹣DE)2,
∴DE=![]() .
.
故答案为![]() .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
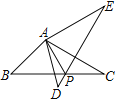
【题目】问题背景:如图,将![]() 绕点
绕点![]() 逆时针旋转60°得到
逆时针旋转60°得到![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,可推出结论:
,可推出结论:![]()
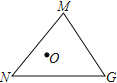
问题解决:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 是
是![]() 内一点,则点
内一点,则点![]() 到
到![]() 三个顶点的距离和的最小值是___________
三个顶点的距离和的最小值是___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4),点P是对角线OB上一个动点,点D的坐标为(0,﹣2),当DP与AP之和最小时,点P的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受非洲猪瘟疫情影响,2019年我国猪肉价格有较大幅度的上升.为了解某地区养殖户的受灾情况,现从该地区建档的养殖户中随机抽取了部分养殖户进行调查(把调查结果分为四个等级:A级-非常严重,B级-严重,C级-一般,D级-没有感染),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
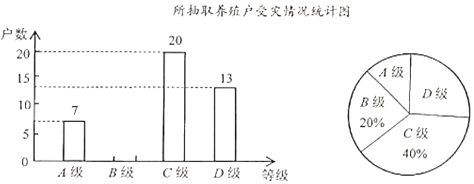
(1)填空:本次抽样调查的养殖户的总户数是______;在扇形统计图中![]() 级所对应的圆心角为______度;
级所对应的圆心角为______度;
(2)请补全条形统计图;
(3)若该地区建档的养殖户有1500户,估计非常严重与严重的养殖户一共有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁两位同学做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人,则第二次传球后球回到甲手里的概率是________;第三次传球后球回到甲手里的概率是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
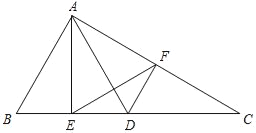
【题目】如图,在△ABC中,点D为边BC上一点,且AD=AB,AE⊥BC,垂足为点E.过点D作DF∥AB,交边AC于点F,连接EF,EF2=![]() BDEC.
BDEC.
(1)求证:△EDF∽△EFC;
(2)如果![]() ,求证:AB=BD.
,求证:AB=BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是⊙O的圆内接四边形,线段AB是⊙O的直径,连结AC.BD.点H是线段BD上的一点,连结AH、CH,且∠ACH=∠CBD,AD=CH,BA的延长线与CD的延长线相交与点P.
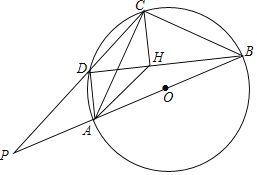
(1)求证:四边形ADCH是平行四边形;
(2)若AC=BC,PB=![]() PD,AB+CD=2(
PD,AB+CD=2(![]() +1)
+1)
①求证:△DHC为等腰直角三角形;②求CH的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,M是圆中![]() 上一定点,P是弦AB上一动点,过点A作射线MP的垂线交圆于点C,连接PC.已知AB=5cm,设A、P两点间的距离为xcm,A、C两点间的距离为y1cm,P、C两点的距离为y2cm.小帅根据学习函数的经验,分别对函数y1、y2随自变量x的变化而变化的规律进行了探究.
上一定点,P是弦AB上一动点,过点A作射线MP的垂线交圆于点C,连接PC.已知AB=5cm,设A、P两点间的距离为xcm,A、C两点间的距离为y1cm,P、C两点的距离为y2cm.小帅根据学习函数的经验,分别对函数y1、y2随自变量x的变化而变化的规律进行了探究.
下面是小帅的探究过程,请补充完整:
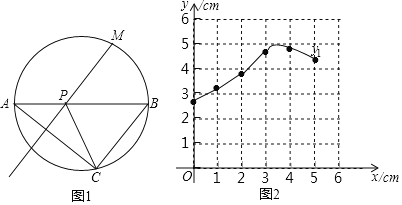
(1)按照表中自变量x的值进行取点,画图、测量,分别得到了y1、y2与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
y1/cm | 2.55 | 3.15 | 3.95 | 4.76 | 4.95 | 4.30 |
y2/cm | 2.55 | 2.64 | 2.67 |
| 1.13 | 2.55 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1、y2的图象;
(3)结合函数图象,解决问题:在点P的运动过程中,当AC与PC的差为最大值时,AP的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交边
交边![]() 于点
于点![]() (点
(点![]() 不与点
不与点![]() 重合),交边
重合),交边![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
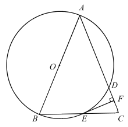
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() .
.
①求![]() 的半径;
的半径;
②连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() _____.
_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com