
【题目】如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上. 
(1)若DE=BF,求证:四边形AFCE是平行四边形;
(2)若四边形AFCE是菱形,求菱形AFCE的周长.
【答案】
(1)解;∵四边形ABCD为矩形,
∴AB=CD,AB∥CD,
∵DE=BF,
∴AF=CE,AF∥CE,
∴四边形AFCE是平行四边形
(2)解;∵四边形AFCE是菱形,
∴AE=CE,
设DE=x,
则AE= ![]() ,CE=8﹣x,
,CE=8﹣x,
则 ![]() =8﹣x,
=8﹣x,
化简有16x﹣28=0,
解得:x= ![]() ,
,
将x= ![]() 代入原方程检验可得等式两边相等,
代入原方程检验可得等式两边相等,
即x= ![]() 为方程的解.
为方程的解.
则菱形的边长为:8﹣ ![]() =
= ![]() ,
,
周长为:4× ![]() =25,
=25,
故菱形AFCE的周长为25
【解析】(1)首先根据矩形的性质可得AB平行且等于CD,然后根据DE=BF,可得AF平行且等于CE,即可证明四边形AFCE是平行四边形;(2)根据四边形AFCE是菱形,可得AE=CE,然后设DE=x,表示出AE,CE的长度,根据相等求出x的值,继而可求得菱形的边长及周长.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
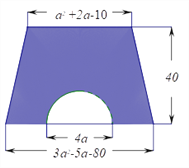
【题目】如图,梯形的上底为![]() +2
+2![]() -10,下底为3
-10,下底为3![]() -5
-5![]() -80,高为40.(
-80,高为40.(![]() 取3)
取3)
(1)用式子表示图中阴影部分的面积;
(2)当![]() =10时,求阴影部分面积的值。
=10时,求阴影部分面积的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】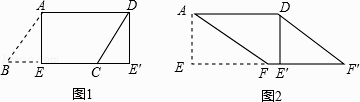
(1)如图1所示,平行四边形纸片ABCD中,AD=5,SABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D是形.
(2)如图2所示,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.
①求证:四边形AFF′D是菱形;
②求四边形AFF′D两条对角线的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D.
(1)若BC=10,BD=6,则点D到AB的距离是多少?
(2)若∠BAD=30°,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列三行数,并完成后面的问题:
①﹣2,4,﹣8,16,﹣32,…;
②l,﹣2,4,﹣8,16,…;
③0,﹣3,3,﹣9,15,…
(1)思考第①行数的规律,写出第n个数字是多少(用含n的式子表示);
(2)第②行数和第①行数有什么关系?第③行数和第②行数又有什么关系?
(3)设x,y,z分别表示第①②③行数的第10个数字,求x+y+z的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(1,0),点B在y轴正半轴上,直线AB与直线l:y=![]() 相交于点C,直线l与x轴交于点D,AB=
相交于点C,直线l与x轴交于点D,AB=![]() .
.
(1)求点D坐标;
(2)求直线AB的函数解析式;
(3)求△ADC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F. 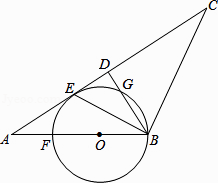
(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)当BD=6,AB=10时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,经过B、D两点的⊙O交AB 于点E,交BC于点F,EB为⊙O的直径. 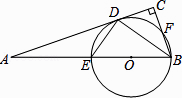
(1)求证:AC是⊙O的切线;
(2)当BC=2,cos∠ABC= ![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com