
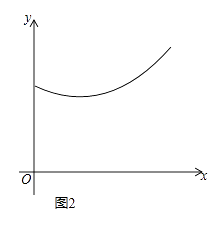
【题目】如图1,在等边△ABC中,点D,E分别是BC,AC边上的中点,点P为AB边上的一个动点,设AP=x,连接PE,PD,PC,DE,其中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是( )
A.线段PE
B.线段PD
C.线段PC
D.线段DE
【答案】A
【解析】解:设等边三角形边长为1,则0≤x≤1,
如图1,分别过点E、C、D作AB的垂线,垂足分别为F、G、H,
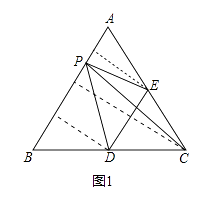
根据等边三角形的性质可知,
当x= ![]() 时,线段PE有最小值;
时,线段PE有最小值;
当x= ![]() 时,线段PC有最小值;
时,线段PC有最小值;
当x= ![]() 时,线段PD有最小值;
时,线段PD有最小值;
∵点E、D分别是AC,BC边的中点
∴线段DE的长为定值 ![]() .
.
根据图2可知,当x= ![]() 时,函数有最小值,故这条线段为PE.
时,函数有最小值,故这条线段为PE.
所以答案是:A.
【考点精析】解答此题的关键在于理解函数的图象的相关知识,掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值.


科目:初中数学 来源: 题型:
【题目】小区规划一个长70m、宽30m的长方形草坪上修建三条同样宽的甬道,使其中两条与AB平行,另一条与BC平行,场地其余部分种草,甬道的宽度为xm.
(1)用含x的代数式表示草坪的总面积S;
(2)如果每一块草坪的面积都相等,且甬道的宽为1m,那么每块草坪的面积是多少平方米?(精确到0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“六城”同创活动中,为努力把我市建成“国家园林城市”,绿化公司计划购买A,B,C三种绿化树共800株,用20辆货车一次运回,对我市城区新建道路进行绿化.按计划,20辆货车都要装运,每辆货车只能装运同一种绿化树,且必须装满.根据下表提供的信息,解答以下问题:
绿 化 树 品 种 | A | B | C |
每辆货车运载量(株) | 40 | 48 | 32 |
每株树苗的价格(元) | 20 | 50 | 30 |
(1)设装运A种绿化树的车辆数为x,装运B种绿化树的车辆数为y,求y与x之间的函数关系式;
(2)如果装运每种绿化树的车辆数都不多于8辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若在“六城”同创活动中要求“厉行节约”办实事,则应采用(2)中的哪种安排方案?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() (x>0)的图象相交于A(2,3),B(a,1)两点.
(x>0)的图象相交于A(2,3),B(a,1)两点.
(1)求这两个函数表达式;
(2)求证:AB=2BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程mx2﹣4x﹣m+5=0,有以下说法:
①当m=0时,方程只有一个实数根;②当m=1时,方程有两个相等的实数根;③当m=﹣1时,方程没有实数根.则其中正确的是( )
A.①②
B.①③
C.②③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l经过平面直角坐标系的原点O,且与x轴正方向的夹角是30°,点A的坐标是(0,1),点B在直线l上,且AB∥x轴,则点B的坐标是 , 现将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线l上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线l上,顺次旋转下去…,则点A6的横坐标是 . 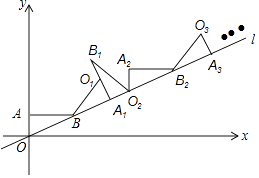
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A、B、C三个点对应的数分别是a、b、c,且满足|a+24|+|b+10|+(c-10)2=0;动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
![]()
(1)求a、b、c的值;
(2)若点P到A点距离是到B点距离的2倍,求点P的对应的数;
(3)当点P运动到B点时,点Q从A点出发,以每秒2个单位的速度向C点运动,Q点到达C点后.再立即以同样的速度返回,运动到终点A,在点Q开始运动后第几秒时,P、Q两点之间的距离为8?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地管辖A,B,C,D四个镇,其中C,A,D三个镇在一条直线上,相互两镇之间的公路里程如图所示,由于大山阻隔,原来从A,C两镇去D镇都需绕到B镇前往.为了发展经济,缩短A,C两镇到D镇的路程,现决定开凿隧道修通A,C两镇直达D镇的公路AD.公路修通后从A镇去D镇的路程比原来缩短了多少千米?(参考数据:![]() =32,
=32,![]() ≈46.65)
≈46.65)
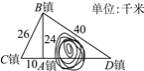
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连接CB,CP.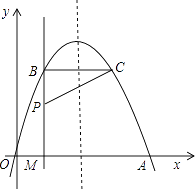
(1)当m=3时,求点A的坐标及BC的长;
(2)当m>1时,连接CA,问m为何值时CA⊥CP?
(3)过点P作PE⊥PC且PE=PC,问是否存在m,使得点E落在坐标轴上?若存在,求出所有满足要求的m的值,并定出相对应的点E坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com