
【题目】已知某服装厂现有甲种布料50米,乙种布料27米,现计划用这两种布料生产A,B两种型号的时装共60套. 已知做一套A型号的时装需用甲种布料1米,乙种布料0.2米,可获利30元;做一套B型号的时装需用甲种布料0.5米,乙种布料0.8米,可获利20元. 设生产A型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
(1)求y(元)与x(套)之间的函数表达式,并求出自变量的取值范围.
(2)当生产A型号的时装多少套时,能使该厂所获利润最大?最大利润是多少?
【答案】(1)![]() ;(2)当生产A型号的时装40套时,能使该厂所获利润最大,最大利润是1600元.
;(2)当生产A型号的时装40套时,能使该厂所获利润最大,最大利润是1600元.
【解析】1)关系式为:B种型号的时装件数×1+A种型号的时装件数×0.5≤50;B种型号的时装件数×0.2+A种型号的时装件数×0.8≤27;
(2)根据(1)中的结果得到结论.
解:(1)![]()
根据题意,得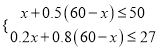
解得 ![]()
∵x是整数
∴x=35,36,37,38,39,40
∴y与x之间的函数表达式为![]()
(2)∵k=10>0
∴y随x的增大而增大
∴当x=40时,y有最大值为10×40+1200=160
答:当生产A型号的时装40套时,能使该厂所获利润最大,最大利润是1600元.
“点睛”此题是一道方案设计题,有一定的开放性.解决本题的关键是读懂题意,找到符合题意的不等关系:加工服装所用布料不大于布料总数,列不等式解答即可.


科目:初中数学 来源: 题型:
【题目】用配方法解方程x2﹣4x﹣6=0,变形正确的是( )
A. (x﹣2)2=2 B. (x﹣2)2=10 C. (x﹣4)2=22 D. (x+2)2=10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有三个内角相等的四边形叫三等角四边形.
(1)三等角四边形ABCD中,∠A=∠B=∠C,求∠A的取值范围;
(2)如图,折叠平行四边形纸片DEBF,使顶点E,F分别落在边BE,BF上的点A,C处,折痕分别为DG,DH.求证:四边形ABCD是三等角四边形.
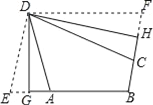
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形网格中,△AOB的顶点均在格点上.
(1)B点关于y轴的对称点的坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)平移过程中,线段OA所扫过的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①所有有理数都能用数轴上的点表示;②符号不同的两个数互为相反数;③有理数包括正数、零和负数;④两数相加,和一定大于任意一个加数,其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣2,a),B(﹣1,b),C(3,c)均在抛物线y=﹣2(x+1)2+3上,则a,b,c的大小关系为( )
A. a<c<b B. b<a<c C. c<a<b D. a<b<c
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com