
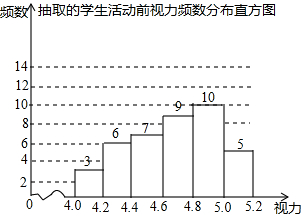
 为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示
为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示 | 分组 | 频数 |
| 4.0≤x<4.2 | 2 |
| 4.2≤x<4.4 | 3 |
| 4.4≤x<4.6 | 5 |
| 4.6≤x<4.8 | 8 |
| 4.8≤x<5.0 | 17 |
| 5.0≤x<5.2 | 5 |
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
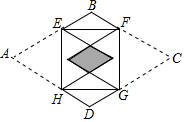 如图,矩形EFGH的四个顶点分别在菱形ABCD的四条边上,BE=BF.将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的$\frac{1}{16}$时,则$\frac{AE}{EB}$为( )
如图,矩形EFGH的四个顶点分别在菱形ABCD的四条边上,BE=BF.将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的$\frac{1}{16}$时,则$\frac{AE}{EB}$为( )| A. | $\frac{5}{3}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知矩形ABCD满足AB:BC=1:$\sqrt{2}$,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
如图,已知矩形ABCD满足AB:BC=1:$\sqrt{2}$,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )| A. | 4$\sqrt{2}$ | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com