
【题目】为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲 | 乙 | 丙 | |
单价(元/棵) | 14 | 16 | 28 |
合理用地(m2/棵) | 0.4 | 1 | 0.4 |

【答案】(1)y=﹣2x2+36x(0<x<18);(2)x的值为10;(3)这批植物不可以全部栽种到这块空地上.
【解析】
(1)根据矩形的面积公式计算即可;
(2)构建方程即可解决问题,注意检验是否符合题意;
(3)利用二次函数的性质求出y的最大值,设购买了乙种绿色植物a棵,购买了丙种绿色植物b棵,由题意:14(400﹣a﹣b)+16a+28b=8600,可得a+7b=1500,推出b的最大值为214,此时a=2,再求出实际植物面积即可判断.
(1)y=x(36﹣2x)=﹣2x2+36x(0<x<18);
(2)由题意:﹣2x2+36x=160,
解得x=10或8,
∵x=8时,36﹣16=20<18,不符合题意,
∴x的值为10;
(3)∵y=﹣2x2+36x=﹣2(x﹣9)2+162,
∴x=9时,y有最大值162,
设购买了乙种绿色植物a棵,购买了丙种绿色植物b棵,
由题意:14(400﹣a﹣b)+16a+28b=8600,
∴a+7b=1500,
∴b的最大值为214,此时a=2,
需要种植的面积=0.4×(400﹣214﹣2)+1×2+0.4×214=162.8>162,
∴这批植物不可以全部栽种到这块空地上.


科目:初中数学 来源: 题型:
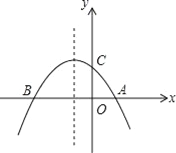
【题目】如图,已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
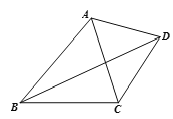
【题目】如图,给出五个等量关系:①AD=BC;②AC=BD;③CE=DE;④∠D=∠C;⑤∠DAB=∠CBA.

请你以其中两个为条件,另外三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明.
已知:
求证:
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
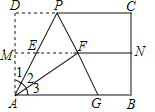
【题目】如图,对折矩形纸片ABCD,使AB与DC重合,得到折痕MN,将纸片展平;再一次折叠,使点D落到MN上的点F处,折痕AP交MN于E;延长PF交AB于G.求证:
(1)△AFG≌△AFP;
(2)△APG为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:已知α、β均为锐角,tanα=![]() ,tanβ=
,tanβ=![]() ,求α+β的度数.
,求α+β的度数.
探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为1),请借助这个网格图求出α+β的度数;
延伸:(2)设经过图中M、P、H三点的圆弧与AH交于R,求![]() 的弧长.
的弧长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC的三边长分别为6 cm、7.5 cm、9 cm,三角形DEF的一边长为4 cm.当三角形DEF的另两边长是下列哪一组时,这两个三角形相似( )
A. 2 cm、3 cm B. 4 cm、5 cm C. 5 cm、6 cm D. 6 cm、7 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠DCB=123°,∠ABC=50°,并且∠BAD+∠CAD=180°,那么∠DAC的度数为_________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
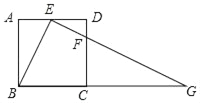
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )

A. 21.7米 B. 22.4米 C. 27.4米 D. 28.8米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com