
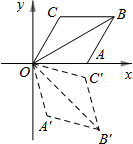
 如图,已知菱形OABC的一边OA在x轴上,OA∥BC,OC∥AB,且OA=AB=BC=CO,将菱形OABC变换到菱形OA′B′C′的位置,若OB=OB′=2$\sqrt{3}$,∠C=120°,∠BOB′=75°,则点B′的坐标为( )
如图,已知菱形OABC的一边OA在x轴上,OA∥BC,OC∥AB,且OA=AB=BC=CO,将菱形OABC变换到菱形OA′B′C′的位置,若OB=OB′=2$\sqrt{3}$,∠C=120°,∠BOB′=75°,则点B′的坐标为( )| A. | (3,$\sqrt{3}$) | B. | (3,-$\sqrt{3}$) | C. | ($\sqrt{6}$,$\sqrt{6}$) | D. | ($\sqrt{6}$,-$\sqrt{6}$) |
分析 首先根据菱形的性质,即可求得∠AOB的度数,又由将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置,可求得∠B′OA的度数,然后在Rt△B′OF中,利用三角函数即可求得OF与B′F的长,则可得点B′的坐标.
解答 解:过点B作BE⊥OA于E,过点B′作B′F⊥OA于F,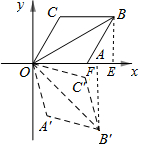
∴∠BE0=∠B′FO=90°,
∵四边形OABC是菱形,
∴OA∥BC,∠AOB=$\frac{1}{2}$∠AOC,
∴∠AOC+∠C=180°,
∵∠C=120°,
∴∠AOC=60°,
∴∠AOB=30°,
∵菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置,
∴∠BOB′=75°,OB′=OB=2$\sqrt{3}$,
∴∠B′OF=45°,
在Rt△B′OF中,
OF=OB′•cos45°=2$\sqrt{3}$×$\frac{\sqrt{2}}{2}$=$\sqrt{6}$,
∴B′F=$\sqrt{6}$,
∴点B′的坐标为:($\sqrt{6}$,-$\sqrt{6}$).
故选:D.
点评 此题考查了平行四边形的性质,旋转的性质以及直角三角形的性质与三角函数的性质等知识.此题综合性较强,难度适中,解题的关键是注意数形结合思想的应用.


科目:初中数学 来源: 题型:解答题
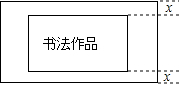 如图,现有一幅书法作品(图中阴影部分所示)需要装裱,已知该书法作品的长为50cm,宽为30cm,上、下边衬等宽、左、右边衬等宽,并且上、下边衬的宽与左、右边衬的宽比为1:2,已知装裱后的作品的面积为2800cm2.
如图,现有一幅书法作品(图中阴影部分所示)需要装裱,已知该书法作品的长为50cm,宽为30cm,上、下边衬等宽、左、右边衬等宽,并且上、下边衬的宽与左、右边衬的宽比为1:2,已知装裱后的作品的面积为2800cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $-\frac{5}{12}$ | C. | $-\frac{12}{5}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com