
 如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.
如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.分析 (1)由切线的性质得出∠BME+∠OMB=90°,再由直径得出∠AMB=90°,利用同角的余角相等判断出结论;
(2)由(1)得出的结论和直角,判断出△BME∽△BAM,即可得出结论,
(3)先在Rt△BEM中,用三角函数求出BM,再在Rt△ABM中,用三角函数和勾股定理计算即可.
解答 解:(1)如图 ,连接OM,
,连接OM,
∵直线CD切⊙O于点M,
∴∠OMD=90°,
∴∠BME+∠OMB=90°,
∵AB为⊙O的直径,
∴∠AMB=90°.
∴∠AMO+∠OMB=90°,
∴∠BME=∠AMO,
∵OA=OM,
∴∠MAB=∠AMO,
∴∠BME=∠MAB;
(2)由(1)有,∠BME=∠MAB,
∵BE⊥CD,
∴∠BEM=∠AMB=90°,
∴△BME∽△BAM,
∴$\frac{BM}{AB}=\frac{BE}{BM}$,
∴BM2=BE•AB;
(3)由(1)有,∠BME=∠MAB,
∵sin∠BAM=$\frac{3}{5}$,
∴sin∠BME=$\frac{3}{5}$,
在Rt△BEM中,BE=$\frac{18}{5}$,
∴sin∠BME=$\frac{BE}{BM}$=$\frac{3}{5}$,
∴BM=6,
在Rt△ABM中,sin∠BAM=$\frac{3}{5}$,
∴sin∠BAM=$\frac{BM}{AB}$=$\frac{3}{5}$,
∴AB=$\frac{5}{3}$BM=10,
根据勾股定理得,AM=8.
点评 此题是圆的综合题,主要考查了切线的性质,直径所对的圆周角是直径,相似三角形的性质和判定,三角函数,解本题的关键是判断出,△BME∽△BAM.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
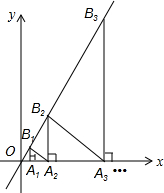 如图,在坐标轴上取点A1(2,0),作x轴的垂线与直线y=2x交于点B1,作等腰直角三角形A1B1A2;又过点A2作x轴的垂线交直线y=2x交于点B2,作等腰直角三角形A2B2A3;…,如此反复作等腰直角三角形,当作到An(n为正整数)点时,则An的坐标是(2×3n-1,0).
如图,在坐标轴上取点A1(2,0),作x轴的垂线与直线y=2x交于点B1,作等腰直角三角形A1B1A2;又过点A2作x轴的垂线交直线y=2x交于点B2,作等腰直角三角形A2B2A3;…,如此反复作等腰直角三角形,当作到An(n为正整数)点时,则An的坐标是(2×3n-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高4$\sqrt{3}$米.(结果保留根号)
如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高4$\sqrt{3}$米.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com