
如图1,四边形ABCD是等腰梯形,AB∥DC,由四个这样的等腰梯形可以拼成如图2所示的平行四边形.
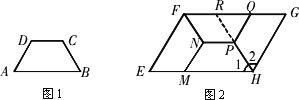
(1)求等腰梯形ABCD的四个内角的度数;
(2)试探究等腰梯形ABCD的四条边之间存在的等量关系,并说明理由;
(3)现有等腰梯形(如图1)若干个,你能利用它们拼出一个菱形吗?若能,请画出大致的示意图.
|
分析:解答第(1)小题时,只要求出∠E的度数即可.解答第(2)小题时,由于容易推得腰与上底相等,所以关键在于找到腰与下底之间的关系. 解:(1)在□EFGH中, 因为EF∥GH, 所以∠E+∠EHG=180°,即∠E+∠1+∠2=180°. 因为∠E、∠1、∠2是三个完全一样的等腰梯形的下底角, 所以∠E=∠1=∠2,∠E=180°÷3=60°. 所以∠A=∠B=60°,∠C=∠D=120°. (2)由于MN既是等腰梯形MNPH的腰,又是等腰梯形EFNM的上底, 所以等腰梯形ABCD的上底与腰相等 为探究等腰梯形ABCD的下底与腰的关系,应延长HP交FQ于点R. 因为∠QPR=180°-∠HPQ=60°=∠PQR, 所以△PQR为等边三角形.所以RQ=PQ. 因为∠FNP=∠HPN=120°,所以FN∥PR. 又NP∥FR,所以四边形FNPR是平行四边形. 所以FR=PN=PQ.所以FQ=FR+RQ=2PQ. 所以等腰梯形ABCD的下底等于腰的2倍. 综上,等腰梯形ABCD的四条边之间的等量关系为AD=DC=BC= (3)能拼出菱形如图,且拼法不唯一.
|


科目:初中数学 来源: 题型:
 足分别为E、F,得四边形DECF,设DE=x,DF=y.
足分别为E、F,得四边形DECF,设DE=x,DF=y.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( )
如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com