
【题目】已知函数y1=x(x≥0),y2=![]() (x>0)的图象如图所示,则以下结论:
(x>0)的图象如图所示,则以下结论:
①两函数图象的交点A的坐标为(2,2);②当x>2时,y1>y2;
③BC=2;④两函数图象构成的图形是轴对称图形;
⑤当x逐渐增大时,y1随着x的增大而增大,y2随着x的增大而减小.
其中正确结论的序号是____________.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,O为正方形对角线的交点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
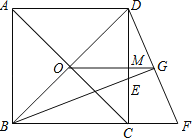
(1)求证:△BCE≌△DCF.
(2)判断OG与BF有什么关系,证明你的结论.
(3)若DF2=8-4![]() ,求正方形ABCD的面积?
,求正方形ABCD的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】概念学习
规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,例如2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作“﹣3的圈4次方”,一般地,把![]() (a≠0)记作
(a≠0)记作![]() a
a![]() ,读作“a的圈n次方”.
,读作“a的圈n次方”.
初步探究
(1)直接写出计算结果:2③=________,![]() =________;
=________;
(2)关于除方,下列说法错误的是________
A.任何非零数的圈2次方都等于1; B.对于任何正整数n,1![]() =1;
=1;
C.3④=4③ ; D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.
深入思考
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?

(1)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.
(﹣3)④=________;5⑥=________;![]() =________.
=________.
(2)想一想:将一个非零有理数a的圈n次方写成幂的形式等于________;
(3)算一算:24÷23+(-16)×2④.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂仓库储存了部分原料,按原计划每时消耗2 t,可用60 h.由于技术革新,实际生产能力有所提高,即每时消耗的原料量大于计划消耗的原料量.设现在每时消耗原料x(单位:t),库存的原料可使用的时间为y(单位:h).
(1)写出y关于x的函数解析式,并求出自变量的取值范围;
(2)若恰好经过24 h才有新的原料进厂,为了使机器不停止运转,则x应控制在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
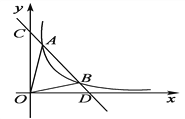
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b-![]() <0时x的取值范围;
<0时x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当m为何值时,关于x的一元二次方程(2m+1)x2+4mx+2m﹣3=0.
(1)有两个不相等的实数根;
(2)有两个相等的实数根;
(3)没有实数根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com