
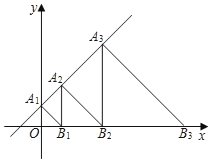
【题目】如图,直线L:y=x+1交y轴于点A1,在x轴正方向上取点B1,使OB1=OA1;过点B1作A2B1⊥x轴,交L于点A2,在x轴正方向上取点B2,使B1B2=B1A2;过点B2作A3B2⊥x轴,交L于点A3,在x轴正方向上取点B3,使B2B3=B2A3;…记△OA1B1面积为S1,△B1A2B2面积为S2,△B2A3B3面积为S3,…则S2019等于_____.
【答案】24035.
【解析】
根据已知条件得到△OA1B1,△B1A2B2,△B2A3B3是等腰直角三角形,根据直线的解析式得到A1(0,1),求得B1(1,0),得到OB1=OA1=1,根据三角形的面积公式得到S1,同理S2,S3,…,进而可得Sn=![]() 22n-2=22n-3,于是得到结论.
22n-2=22n-3,于是得到结论.
∵OB1=OA1;过点B1作A2B1⊥x轴,B1B2=B1A2;A3B2⊥x轴,B2B3=B2A3;…
∴△OA1B1,△B1A2B2,△B2A3B3是等腰直角三角形,
∵y=x+1交y轴于点A1,
∴A1(0,1),
∴B1(1,0),
∴OB1=OA1=1,
∴S1=![]() ×1×1=
×1×1=![]() ×12,
×12,
同理S2=![]() ×2×2=
×2×2=![]() 22,S3=
22,S3=![]() 4×4=
4×4=![]() 42;…
42;…
∴Sn=![]() 22n﹣2=22n﹣3,
22n﹣2=22n﹣3,
∴S2019=22×2019﹣3=24035
故答案为24035.


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
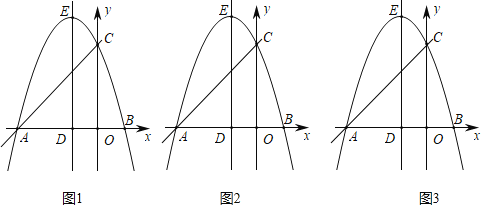
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线y=a(x﹣![]() )(x+
)(x+![]() )与x轴交于A、B两点,与y轴交于点C,直线DE是抛物线的对称轴,点D在x轴上,点E在抛物线上,直线y=kx+
)与x轴交于A、B两点,与y轴交于点C,直线DE是抛物线的对称轴,点D在x轴上,点E在抛物线上,直线y=kx+![]() 过点A、C.
过点A、C.
(1)求抛物线的解析式;
(2)点P是第二象限对称轴左侧抛物线上一点,过点P作PQ∥AC交对称轴于点Q,设点P的横坐标为t,线段QD的长为d,求d与t的函数解析式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,直线AC与对称轴交于点F,点M在对称轴ED上,连接AM、AE,∠AMD=2∠EAM,过点A作AG⊥AM交过点D平行于AE的直线于点G,点N是线段BP延长线上一点,连接AN、MN、NF,若四边形NMGA与四边形NFDA的面积相等,且FN∥AM,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边)
的左边)![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,点
,点![]() 为抛物线的顶点.
为抛物线的顶点.
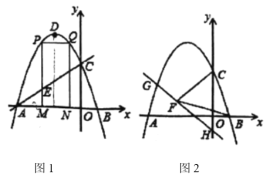
(1)求抛物线的解析式;
(2)点![]() 为线段
为线段![]() 上一点(点
上一点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,与直线
轴的垂线,与直线![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() ,过点
,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,可得矩形
,可得矩形![]() ,如图1,点
,如图1,点![]() 在点
在点![]() 左边,当矩形
左边,当矩形![]() 的周长最大时,求
的周长最大时,求![]() 的值,并求出此时的
的值,并求出此时的![]() 的面积;
的面积;
(3)已知![]() ,点
,点![]() 在抛物线上,连
在抛物线上,连![]() ,直线
,直线![]() ,垂足为
,垂足为![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人利用扑克牌玩“10点”游戏,游戏规则如下:
①将牌面数字作为“点数”,如红桃6的“点数”就是6(牌面点数与牌的花色无关);
②两人摸牌结束时,将所得牌的“点数”相加,若“点数”之和小于或等于10,此时“点数”之和就是“最终点数”,若“点数”之和大于10,则“最终点数”是0;
③游戏结束之前双方均不知道对方“点数”;
④判定游戏结果的依据是:“最终点数”大的一方获胜,“最终点数”相等时不分胜负.
现甲、乙均各自摸了两张牌,数字之和都是5,这时桌上还有四张背面朝上的扑克牌,牌面数字分别是4,5,6,7.

(1)若甲从桌上继续摸一张扑克牌,乙不再摸牌,则甲获胜的概率为 ;
(2)若甲先从桌上继续摸一张扑克牌,接着乙从剩下的扑克牌中摸出一张牌,然后双方不再摸牌,请用树状图或表格表示出这次摸牌后所有可能的结果,再列表呈现甲、乙的“最终点数”,并求乙获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
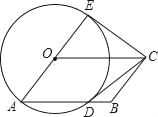
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于点D,延长AO交⊙O于点E,连接CD、CE,若CE是⊙O的切线.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为4,OC=7,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
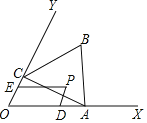
【题目】如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
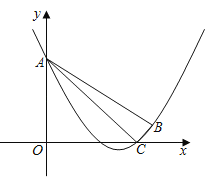
【题目】如图,在平面直角坐标系xOy中,抛物线y=![]() x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
x2+mx+n经过点B(6,1),C(5,0),且与y轴交于点A.
(1)求抛物线的表达式及点A的坐标;
(2)点P是y轴右侧抛物线上的一点,过点P作PQ⊥OA,交线段OA的延长线于点Q,如果∠PAB=45°.求证:△PQA∽△ACB;
(3)若点F是线段AB(不包含端点)上的一点,且点F关于AC的对称点F′恰好在上述抛物线上,求FF′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
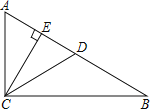
【题目】在直角三角形ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,BC=2![]() ,则AB=_____.
,则AB=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com