
【题目】已知矩形![]() ,
,![]() ,
,![]() ,将它绕着点
,将它绕着点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 度
度![]() 得到矩形
得到矩形![]() ,此时
,此时![]() ,
,![]() 这两边所在的直线分别与
这两边所在的直线分别与![]() 边所在的直线相交于点
边所在的直线相交于点![]() 、
、![]() ,当
,当![]() 时,
时,![]() 的长为________.
的长为________.

【答案】![]()
【解析】
作PH⊥C1D1(如图),证明∴△BPC≌△PQH,根据全等三角形的性质得到PQ=PB,又因DP:DQ=1:2,所以DP=BP=PQ;设DP=x,则BP=x,PC=DC-DP=8-x,在Rt△BCP中,利用勾股定理可得方程(8-x)2+42=x2,解方程求得x=5,即可求得DP的长.
作PH⊥C1D1,如图,
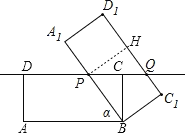
∵矩形ABCD绕着点B按顺时针方向旋转得到矩形A1BC1D1,
∴BC=BC1=4,
易得四边形BPHC1为矩形,
∴PH=BC1,
∴BC=PH,
∵C1D1∥A1B,
∴∠BPC=∠PQH,
在△BPC和△PQH中,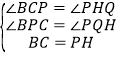 ,
,
∴△BPC≌△PQH,
∴PQ=PB,
∵DP:DQ=1:2,
∴DP=BP=PQ,
设DP=x,则BP=x,PC=DC-DP=8-x,
在Rt△BCP中,(8-x)2+42=x2,解得x=5,
即DP的长为5.
故答案为:5.


科目:初中数学 来源: 题型:
【题目】如图,在电线杆![]() 上的
上的![]() 处引拉线
处引拉线![]() 、
、![]() 固定电线杆,拉线
固定电线杆,拉线![]() 和地面所成的角
和地面所成的角![]() ,在离电线杆
,在离电线杆![]() 米的
米的![]() 处安置高为
处安置高为![]() 米的测角仪
米的测角仪![]() ,在
,在![]() 处测得电线杆上
处测得电线杆上![]() 处的仰角为
处的仰角为![]() ,求拉线
,求拉线![]() 的长(结构保留一位小数,参考数据:
的长(结构保留一位小数,参考数据:![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在线段BC上,若BC=DE,AC=DC,AB=EC,且∠ACE=180°—∠ABC—2x°,则下列角中,大小为x°的角是

A.∠EFCB.∠ABCC.∠FDCD.∠DFC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识生成)我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:

(1)根据图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(3)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+y+z= .
(知识迁移)(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,格点△ABC(顶点是网格线的交点)在平面直角坐标系中的位置如图所示.
(1)将△ABC先向下平移2个单位长度,再向右平移8个单位长度,画出平移后的△A1B1C1,并写出顶点B1的坐标;
(2)作△ABC关于y轴的对称图形△A2B2C2,并写出项点B2的坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】魏晋时期的数学家刘徽首创割圆术.为计算圆周率建立了严密的理论和完善的算法.作圆内接正多边形,当正多边形的边数不断增加时,其周长就无限接近圆的周长,进而可用![]() 来求得较为精确的圆周率.祖冲之在刘徽的基础上继续努力,当正多边形的边数增加24576时,得到了精确到小数点后七位的圆周率,这一成就在当时是领先其他国家一千多年,如图,依据“割圆术”,由圆内接正六边形算得的圆周率的近似值是( )
来求得较为精确的圆周率.祖冲之在刘徽的基础上继续努力,当正多边形的边数增加24576时,得到了精确到小数点后七位的圆周率,这一成就在当时是领先其他国家一千多年,如图,依据“割圆术”,由圆内接正六边形算得的圆周率的近似值是( )

A. 0.5 B. 1 C. 3 D. π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com