
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于二、四象限内的
的图象交于二、四象限内的![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
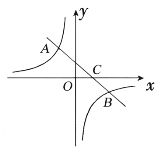
(1)求该反比例函数和一次函数的解析式;
(2)连接![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
(3)设点![]() 在
在![]() 轴上,且满足
轴上,且满足![]() 是直角三角形,直接写出点
是直角三角形,直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)9;(3)存在,满足条件的
;(2)9;(3)存在,满足条件的![]() 点坐标为
点坐标为![]()
【解析】
(1)先把A(-3,4)代入反比例函数解析式得到m的值,从而确定反比例函数的解析式为y=![]() ;再利用反比例函数解析式确定B点坐标为(6,-2),然后运用待定系数法确定所求的一次函数的解析式为y=
;再利用反比例函数解析式确定B点坐标为(6,-2),然后运用待定系数法确定所求的一次函数的解析式为y=![]() ;
;
(2)先依据一次函数求得点C的坐标,进而得到△AOB 的面积;
(3)过A点作AP1⊥x轴交x轴于P1,AP2⊥AC交x轴于P2,即可得P1点的坐标为(-3,0);再证明Rt△AP2P1∽Rt△CAP1,利用相似比计算出P1P2的长度,进而得到OP2的长度,可得P2点的坐标为![]() ,于是得到满足条件的P点坐标.
,于是得到满足条件的P点坐标.
(1)将![]() 代入
代入![]() ,得
,得![]() .
.
∴反比例函数的解析式为![]() ,
,
将![]() 代入
代入![]() ,
,
得![]()
解得![]()
∴![]()
将![]() 分别代入
分别代入![]() ,得
,得
![]() ,解得
,解得
∴所求的一次函数的解析式为![]()
(2)当![]() 时,
时,![]() ,
,
解得:![]() ,
,
![]()
![]()
∴![]()
(3)存在
∴满足条件的![]() 点坐标为
点坐标为![]() ,理由如下:
,理由如下:
过A点作AP1⊥x轴于P1,AP2⊥AC交x轴于P2,如图,
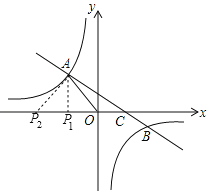
∴∠AP1C=90°,
∵A点坐标为(-3,4),
∴P1点的坐标为(-3,0);
∵∠P2AC=90°,
∴∠P2AP1+∠P1AC=90°,而∠AP2P1+∠P2AP1=90°,
∴∠AP2P1=∠P1AC,
∴Rt△AP2P1∽Rt△CAP1,
∴![]() ,即
,即![]() ,
,
∴P1P2=![]() ,
,
∴OP2=3+![]() =
=![]() ,
,
∴P2点的坐标为(![]() ,0),
,0),
∴满足条件的P点坐标为(-3,0)、(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】今年某水果加工公司分两次采购了一批桃子,第一次费用为25万元,第二次费用为30万元.已知第一次采购时每吨桃子的价格比去年的平均价格上涨了0.1万元,第二次采购时每吨桃子的价格比去年的平均价格下降了0.1万元,第二次采购的数量是第一次采购数量的2倍.
(1)试问去年每吨桃子的平均价格是多少万元?两次采购的总数量是多少吨?
(2)该公司可将桃子加工成桃脯或桃汁,每天只能加工其中一种.若单独加工成桃脯,每天可加工3吨桃子,每吨可获利0.7万元;若单独加工成桃汁,每天可加工9吨桃子,每吨可获利0.2万元.为出口需要,所有采购的桃子必须在30天内加工完毕.
①根据该公司的生产能力,加工桃脯的时间不能超过多少天?
②在这次加工生产过程中,应将多少吨桃子加工成桃脯才能获取最大利润?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界500强H公司决定购买某演唱会门票奖励部分优秀员工,演唱会的购票方式有以下两种,
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元(其中总费用=广告赞助费+门票费);
方式二:如图所示,设购买门票x张,总费用为y万元
(1)求用购票“方式一”时y与x的函数关系式;
(2)若H、A两家公司分别釆用方式一、方式二购买本场演唱会门票共400张,且A公司购买超过100张,两公司共花费27.2万元,求H、A两公司各购买门票多少张?
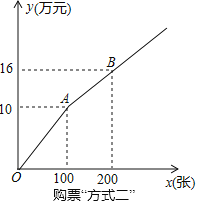
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,点A(2,1).
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点P,使四边形ABOP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师在讲解复习《圆》的内容时,用投影仪屏幕展示出如下内容:
![]()
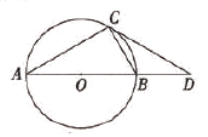
张老师让同学们添加条件后,编制一道题目,并按要求完成下列填空.
(1)在屏幕内容中添加条件![]() ,则
,则![]() 的长为______.
的长为______.
(2)以下是小明、小聪的对话:

参考上面对话,在屏幕内容中添加条件,编制一道题目(此题目不解答,可以添线、添字母).
_________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C,D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为______.
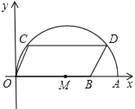
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O交斜边AC于点D,过圆心O作OE∥AC,交BC于点E,连接DE.
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:2DE2=CDOE;
(3)若tanC=![]() ,DE=
,DE=![]() ,求AD的长.
,求AD的长.
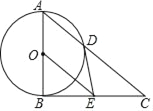
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),直线y=﹣![]() x+
x+![]() 与边AB,BC分别相交于点M,N,函数y=
与边AB,BC分别相交于点M,N,函数y=![]() (x>0)的图象过点M.
(x>0)的图象过点M.
(1)试说明点N也在函数y=![]() (x>0)的图象上;
(x>0)的图象上;
(2)将直线MN沿y轴的负方向平移得到直线M′N′,当直线M′N′与函数y═![]() (x>0)的图象仅有一个交点时,求直线M'N′的解析式.
(x>0)的图象仅有一个交点时,求直线M'N′的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,一架伸缩楼梯托架![]() 固定在墙面上,托架
固定在墙面上,托架![]() 始终与地面垂直且
始终与地面垂直且![]() .如图2, 旋转支撑臂
.如图2, 旋转支撑臂![]() 绕着点
绕着点![]() 旋转,当伸缩楼梯下放时,楼梯长
旋转,当伸缩楼梯下放时,楼梯长![]() 米,点
米,点![]() 正好接触地面,此时,旋转支撑臂
正好接触地面,此时,旋转支撑臂![]() 与楼梯托架
与楼梯托架![]() 之间的夹角为
之间的夹角为![]() ;当伸缩楼梯上收时,旋转支撑臂
;当伸缩楼梯上收时,旋转支撑臂![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() ,楼梯长
,楼梯长![]() 变为
变为![]() 米,此时,楼梯底部的脚垫
米,此时,楼梯底部的脚垫![]() 到地面的距离为( )米.
到地面的距离为( )米.

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com