
【题目】如图,AB是⊙D的直径,AD切⊙D于点A,EC=CB.则下列结论:①BA⊥DA; ②OC∥AE;③∠COE=2∠CAE;④OD⊥AC.一定正确的个数有( )
A.4个
B.3个
C.2个
D.1个
【答案】B
【解析】解:①∵AB是⊙D的直径,AD切⊙D于点A, ∴AD⊥AB;
故①正确;
②∵EC=CB,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]()
![]() ,
,
∴∠COB=∠EAB,
∴OC∥AE;
故②正确;
③∵O是圆心,
∴∠COE=2∠CAE;
故③正确;
④∵点E不一定是AC的中点,
∴OE与AC不一定垂直,
故④不正确;
正确的有①②③,
故选B.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对圆周角定理的理解,了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.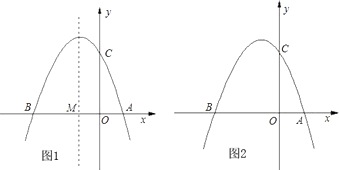
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点![]() ,若点Q的坐标为
,若点Q的坐标为![]() ,其中a为常数,则称点Q是点P的“a级关联点”
,其中a为常数,则称点Q是点P的“a级关联点”![]() 例如,点
例如,点![]() 的“3级关联点”为
的“3级关联点”为![]() ,即
,即![]() .
.
![]() 已知点
已知点![]() 的“
的“![]() 级关联点”是点
级关联点”是点![]() ,点B的“2级关联点”是
,点B的“2级关联点”是![]() ,求点
,求点![]() 和点B的坐标;
和点B的坐标;
![]() 已知点
已知点![]() 的“
的“![]() 级关联点”
级关联点”![]() 位于y轴上,求
位于y轴上,求![]() 的坐标;
的坐标;
![]() 已知点
已知点![]() ,
,![]() ,点
,点![]() 和它的“n级关联点”
和它的“n级关联点”![]() 都位于线段CD上,请直接写出n的取值范围.
都位于线段CD上,请直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个边长为4的等边三角形ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E. 
(1)求CE的长;
(2)求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为方便市民出行,减轻城市中心交通压力,长沙市正在修建贯穿星城南北、东西的地铁1、2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.
(1)求1号线,2号线每千米的平均造价分别是多少亿元?
(2)除1、2号线外,长沙市政府规划到2018年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角梯形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm。点P从点A出发,以每秒3cm的速度沿折线ABCD运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动。已知动点P,Q同时出发,当点Q运动到点C时,P,Q运动停止,设运动时间为t秒.
(1)求CD的长.
(2)t为何值时?四边形PBQD为平行四边形.
(3)在点P,点Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1 , 已知点C1的坐标为(4,0),写出顶点A1 , B1的坐标,并画出△A1B1C1;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3 , 写出△A3B3C3的各顶点的坐标,并画出△A3B3C3 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H. 
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.求证:△AGE≌△AFE; 
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com