Question

若已知关于x的方程（x-2）（x²-4x+m）=0有三个实根．
（1）试求m的取值围；
（2）若这三个实根恰好可以作为一个三角形的三条边的长，求此时m的取值范围．
（3）若这三个实根作成的三角形是等腰三角形，求m值及三角形的面积．

Answer 1

解：（1）x=2是方程的一个根，则方程x²-4x+m=0必须有二个根，
所以，△=b²-4ac=16-4m≥0，
则m≤4．
（2）方程的三个实根为，
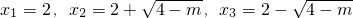
根据三角形的任两边之和必须大于第三边得x₁+x₂＞x₃显然成立；x₂+x₃＞x₁也显然成立；，
又由（1）知m≤4，
所以，要使方程的三个实根作为一个三角形的三条边长的m取值范围为3＜m≤4；
（3）若三角形是等腰三角形，则x₁=x₂或x₁=x₃或x₂=x₃，
可得m=4，此时三角形为边长等于2的等边三角形，
三角形的面积为．
分析：（1）关于x的方程（x-2）（x²-4x+m）=0有三个实根，即x²-4x+m=0有两个实数根，根据一元二次方程根的判别式解答即可；
（2）求出方程的三个根，根据三角形的两边之和大于第三边列不等式解答即可；
（3）根据等腰三角形的性质，令方程的三个根两两相等，据此解答即可．
点评：本题考查了根的判别式、根与系数的关系、三角形的面积、三角形三边关系、等腰三角形的性质等知识，要注意转化，将原方程转化为一元一次方程和一元二次方程来解答．
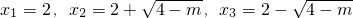