
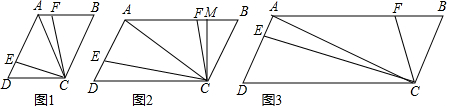
分析 (1)由平行四边形的性质得出∠D=∠B=60°,证出△ABC、△ACD均为等边三角形,得出∠B=∠CAD=∠ACB=60°,BC=AC,证出∠BCF=∠ACE,由ASA证明△AEC≌△BFC即可;
(2)①求出∠BCM=30°,得出BC=2BM,设BM=x,则BC=2x,由勾股定理得出CM=$\sqrt{3}$x,得出AB=2AD=2BC=4x,由勾股定理求出AC=$\sqrt{A{M}^{2}+C{M}^{2}}$=$\sqrt{9{x}^{2}+3{x}^{2}}$=2$\sqrt{3}$x,由勾股定理的逆定理得出∠ACB=90°即可;
②证出∠MCF=∠ACE,∠CAE=90°,证明△ACE∽△MCF,得出$\frac{AE}{FM}$=$\frac{AC}{CM}$=$\frac{2\sqrt{3}x}{\sqrt{3}x}$=2,即可得出结论;
(3)作CN⊥AB于点N,CH⊥AD于点H,CH与AB交于点M,证出∠HAM=∠MCN,由平行四边形的性质得出∠HAM=∠MCN=60°,求出∠ECH=∠FCN,证明△CFN∽△CEH,得出$\frac{CF}{CE}$=$\frac{CN}{CH}$,由平行四边形的面积关系得出CH=3CN,即可得出结论.
解答 (1)证明:∵四边形ABCD是平行四边形,∠BCD=120°,
∴∠D=∠B=60°,AB=CD,AD=BC,
∵AB=AD,
∴△ABC、△ACD均为等边三角形,
∴∠B=∠CAD=∠ACB=60°,BC=AC,
∵∠ECF=60°,
∴∠BCF=∠ACE,
在△AEC和△BFC中,$\left\{\begin{array}{l}{∠B=∠CAE}\\{BC=AC}\\{∠BCF=∠ACE}\end{array}\right.$,
∴△AEC≌△BFC(ASA);
(2)证明:①∵CM⊥AB,∠B=60°,
∴∠BCM=30°,
∴BC=2BM,
设BM=x,则BC=2x,CM=$\sqrt{B{C}^{2}-B{M}^{2}}$=$\sqrt{4{x}^{2}-{x}^{2}}$=$\sqrt{3}$x,
∴AB=2AD=2BC=4x,
∴AM=3x,
∵CM⊥AB,
∴AC=$\sqrt{A{M}^{2}+C{M}^{2}}$=$\sqrt{9{x}^{2}+3{x}^{2}}$=2$\sqrt{3}$x,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴AC⊥BC;
②∵AC⊥BC,∠BCM=30°,
∴∠ACM=60°,
∵∠ECF=60°,
∴∠MCF=∠ACE,
∵AC⊥BC,四边形ABCD是平行四边形,
∴∠CAE=90°,
∴∠CMF=∠CAE=90°,
∴△ACE∽△MCF,
∴$\frac{AE}{FM}$=$\frac{AC}{CM}$=$\frac{2\sqrt{3}x}{\sqrt{3}x}$=2,
∴AE=2FM;
(3)解:作CN⊥AB于点N,CH⊥AD于点H,CH与AB交于点M,如图所示:
∴∠HAM+∠AMH=∠NCM+∠CMN=90°,
∵∠AMH=∠CMN,
∴∠HAM=∠MCN,
∵四边形ABCD是平行四边形,∠BCD=120°,
∴∠HAM=∠MCN=60°,
∵∠ECF=60°,
∴∠ECH=∠FCN,
∴△CFN∽△CEH,
∴$\frac{CF}{CE}$=$\frac{CN}{CH}$,
∵平行四边形ABCD的面积=AB•CN=AD•CH,AB=3AD,
∴CH=3CN,
∴$\frac{CF}{CE}$=$\frac{CN}{CH}$=$\frac{1}{3}$,
∴CE=3CF.
点评 本题是四边形综合题目,考查了平行四边形的性质、全等三角形的判定与性质、勾股定理、勾股定理的逆定理、相似三角形的判定与性质等知识;本题综合性强,有一定难度.


科目:初中数学 来源: 题型:解答题
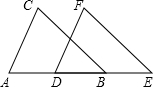 把下面的推理过程补充完整,并在括号内注明理由
把下面的推理过程补充完整,并在括号内注明理由查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元,每天可售出40件,若每件降价10元,则每天多售出10件,请根据以上信息解答下列问题:
某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元,每天可售出40件,若每件降价10元,则每天多售出10件,请根据以上信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com