
分析 (1)根据x的取值范围结合绝对值的意义解答即可;
(2)根据x的取值范围结合绝对值的意义分情况进行计算.
解答 解:(1)|x-1|表示的几何意义是:数轴上表示数1的点之间的距离;
故答案为:数轴上表示数1的点之间的距离;
(2)要使|x-1|+|x+2|的值最小,x的值只要取-2到1之间(包括-2、1)的任意一个数,
当x=-2时,|x-1|+|x+2|=3;
当x=1时,|x-1|+|x+2|=3;
当x=0时,|x-1|+|x+2|=3;
当x=-1时,|x-1|+|x+2|=3.
所以|x-1|+|x+2|的最小值是3.
点评 本题考查了绝对值,注意到线段两端点距离最小的点在线段上(端点除外).


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
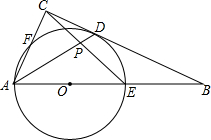 在Rt△ABC中,∠ACB=90°,O在AB上,⊙经过点A,与CB切于D,分别交AB、AC于E、F.
在Rt△ABC中,∠ACB=90°,O在AB上,⊙经过点A,与CB切于D,分别交AB、AC于E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,M是△ABC的边BC上一点,△BME旋转后能与△CMF重合,已知∠ABC=∠ACF,∠EBM=28°,∠ACB=66°,求∠BAC的度数.
如图,M是△ABC的边BC上一点,△BME旋转后能与△CMF重合,已知∠ABC=∠ACF,∠EBM=28°,∠ACB=66°,求∠BAC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
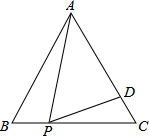 如图,在等边三角形ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=$\frac{2}{3}$,则△ABC的边长为3.
如图,在等边三角形ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=$\frac{2}{3}$,则△ABC的边长为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知在Rt△ABC中,∠BAC=90°,AD⊥BC于D,CE为∠ACB的平分线交AD于E,AF为∠BAD的平分线,交BC于F,求证:△ACE≌△FCE.
如图,已知在Rt△ABC中,∠BAC=90°,AD⊥BC于D,CE为∠ACB的平分线交AD于E,AF为∠BAD的平分线,交BC于F,求证:△ACE≌△FCE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=5y+5×10}\\{x=6y-6×2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=5y-5×10}\\{x=6y+6×2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x=5y-10}\\{x=6y+2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5y+10}\\{x=6y-2}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com