
【题目】如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,AF=4,CF=2,求AE的长.
【答案】
(1)证明:如图,连接CD,
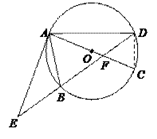
∵AC是⊙O的直径,
∴∠ADC=90°.
∴∠ADB+∠EDC =90°
∵∠BAC=∠EDC, ∠EAB =∠ADB,
∴∠EAC=∠EAB+∠BAC=90°,
∴EA是⊙O的切线;
(2)如图,连接BC
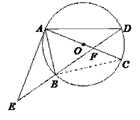
∵AC是⊙O的直径,
∴∠ABC=90°.
∴∠CBA=∠ABC =90°.
∵B是EF的中点,
∴在Rt△EAF中,AB=BF.
∴∠BAC=∠AFE
∴△EAF∽△CBA.
∴ ![]() ,
,
∵AF=4,CF=2,
∴AC=6,EF=2AB.
∴ ![]() ,解得AB=
,解得AB= ![]() ,
,
∴EF= ![]() .
.
∴AE= ![]()
【解析】(1)连接CD,由AC是⊙O的直径,得出∠ADC=90°,由角的关系可求出∠EAC=90°,即可证出EA是⊙O的切线。
(2)连接BC,由AC是⊙O的直径,可得出∠ABC=90°,由在Rt△EAF中,B是EF的中点,可得出∠BAC=∠AFE,就可证出△EAF∽△CBA,得对应边成比例,求出AB、EF的长,然后利用勾股定理即可求出AE的长。


科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F; B. ∠B=∠E; C. BC∥EF ; D. ∠A=∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
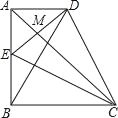
【题目】如图,四边形ABCD中,∠DAB=∠ABC=90°,AB=BC,E是AB的中点,CE⊥BD.
(1)求证:BE=AD;
(2)求证:AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(列二元一次方程组解应用题)某公司共有3个一样规模的大餐厅和2个一样规模的小餐厅,经过测试同时开放2个大餐厅和1个小餐厅,可供300名员工就餐;同时开放1个大餐厅,1个小餐厅,可供170名员工就餐.
(1)请问1个大餐厅、1个小餐厅分别可供多少名员工就餐;
(2)如果3个大餐厅和2个小餐厅全部开放,那么能否供全体450名员工就餐?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知1+2+1=4=22,1+2+3+2+1=9=32,1+2+3+4+3+2+1=16=42,1+2+3+4+5+4+3+2+1=25=52.根据上面四式的计算规律求:1+2+3+…+2014+2015+2016+2015+2014+…+3+2+1=________(写出某数的平方即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y= ![]() +bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( ).
+bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( ).
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两汽车,甲从A地去B地,乙从B地去A地,同时相向而行,1.5小时后两车相遇.相遇后,甲车还需要2小时到达B地,乙车还需要![]() 小时到达A地.若A、B两地相距210千米,试求甲乙两车的速度.
小时到达A地.若A、B两地相距210千米,试求甲乙两车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
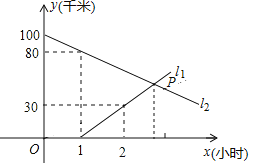
【题目】A,B两地相距100千米,甲,乙两人骑车分别从A,B两地相向而行,图中![]() 和
和![]() 分别表示他们各自到A地的距离
分别表示他们各自到A地的距离![]() 千米
千米![]() 与时间
与时间![]() 小时
小时![]() 的关系,根据图中提供的信息,解答下列问题:
的关系,根据图中提供的信息,解答下列问题:
![]() 图中哪条线表示甲到A地的距离与时间的关系?
图中哪条线表示甲到A地的距离与时间的关系?
![]() 甲,乙两人的速度分别是多少?
甲,乙两人的速度分别是多少?
![]() 求P点的坐标,并解释P点的实际意义.
求P点的坐标,并解释P点的实际意义.
![]() 甲出发多长时间后,两人相距30千米?
甲出发多长时间后,两人相距30千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com