
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,AC交DE于点F.
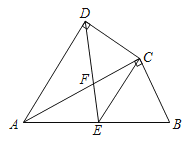
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=5,AB=6,求![]() 的值.
的值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)欲证明AC2=ABAD,只要证明△DCA∽△CBA;
(2)根据直角三角形斜边中线的性质可知EC=EA=EB,推出∠DAC=∠EAC=∠ACE即可证明;
(3)由AD∥CE,可得![]() ,由此即可解决问题.
,由此即可解决问题.
(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
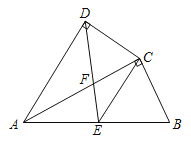
∵∠ADC=∠ACB=90°,
∴△DCA∽△CBA,
∴![]() ,
,
∴AC2=ABAD.
(2)∵∠ACB=90°,AE=EB,
∴CE=AE=EB,
∴∠EAC=∠ECA,
∵∠DAC=∠CAE,
∴∠DAC=∠ACE,
∴AD∥EC.
(3)∵∠ACB=90°,AE=EB,
∴CE=![]() AB=3,AD∥CE,
AB=3,AD∥CE,
∴![]() ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
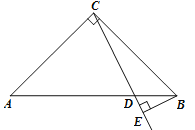
【题目】如图,已知Rt△ABC中,∠ACB=90°,AC=BC,D是线段AB上的一点(不与A、B重合).过点B作BE⊥CD,垂足为E.将线段CE绕点C顺时针旋转![]() ,得到线段CF,连结EF.设∠BCE度数为
,得到线段CF,连结EF.设∠BCE度数为![]() .
.
(1)①补全图形;
②试用含![]() 的代数式表示∠CDA.
的代数式表示∠CDA.
(2)若![]() ,求
,求![]() 的大小.
的大小.
(3)直接写出线段AB、BE、CF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
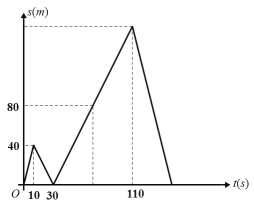
【题目】星期一升旗仪式前,李雷和韩梅梅两位数学课代表因为清 查作业耽搁了时间,打算匀速从教室跑到600 米外的中心广场 参加升旗仪式,出发时李雷发现鞋带松了,停下来系鞋带,韩 梅梅继续跑往中心广场,李雷系好鞋带后立即沿同一路线开始 追赶韩梅梅,李雷在途中追上韩梅梅后,担心迟到继续以原速 度往前跑,李雷到达操场时升旗仪式还没有开始,于是李雷站 在广场等待,韩梅梅继续跑往中心广场.设李雷和韩梅梅两人相距 s (米 ) ,韩梅梅跑步的时间为 t (秒), s 关于 t 的函数图象如图所示,则在整个运动过程 中,李雷和韩梅梅第一次相距 80 米后,再过_____秒钟两人再次相距 80 米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在梯形ABCD中,AB∥CD,CE平分∠BCD,CE⊥AD于E,DE=2AE.若△CED面积为1,则四边形ABCE的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
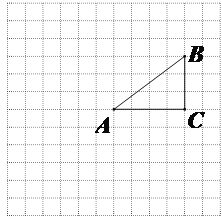
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
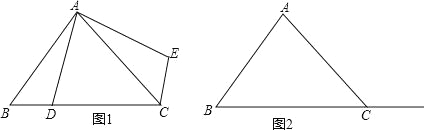
【题目】在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到AE,连结EC.如果AB=AC,∠BAC=90°.
①当点D在线段BC上时(与点B不重合),如图1,请你判断线段CE、BD之间的位置和数量关系(直接写出结论);
②当点D在线段BC的延长线上时,请你在图2画出图形,判断①中的结论是否仍然成立,并证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“垃圾分类”越来越受到人们的关注,我市某中学对部分学生就“垃圾分类”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:
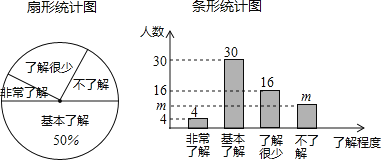
(1)接受问卷调查的学生共有 人,条形统计图中![]() 的值为 ;
的值为 ;
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为 ;
(3)若从对垃圾分类知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加垃圾分类知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
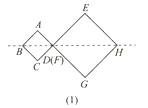
【题目】如图所示,四边形ABCD是边长为1的正方形,四边形EFGH是边长为2的正方形,点D与点F重合,点B、D(F)、H在同一条直线上.将正方形ABCD沿F→H方向平移到点B与点H重合时停止.设点D,F之间的距离为x,正方形ABCD与正方形EFGH重叠部分的面积为y,则能大致反映y与x之间函数关系的图像是( ).


A. 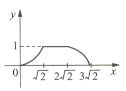 B.
B. 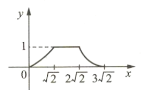 C.
C. 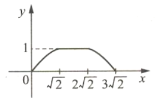 D.
D. 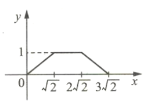
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com