
分析 由关于x的不等式组$\left\{\begin{array}{l}{5x-3a≥3(x+a)+4}\\{2a-x≥2x-4(a+1)-5}\end{array}\right.$有解,可得a≤1,由关于x的函数y=(a-1)x2+2$\sqrt{3}$x+a+1与x轴有且只有一个交点,可得a=±2,继而利用概率公式即可求得答案.
解答 解:$\left\{\begin{array}{l}{5x-3a≥3(x+a)+4①}\\{2a-x≥2x-4(a+1)-5②}\end{array}\right.$,
由①得:x≥3a+2,
由②得:x≤2a+3,
∴当3a+2≤2a+3,即a≤1时,关于x的不等式组$\left\{\begin{array}{l}{5x-3a≥3(x+a)+4}\\{2a-x≥2x-4(a+1)-5}\end{array}\right.$有解;
∵y=(a-1)x2+2$\sqrt{3}$x+a+1与x轴有且只有一个交点,
∴△=(2$\sqrt{3}$)2-4(a-1)(a+1)=16-4a2=0,
解得:a=±2,
∴使得关于x的不等式组$\left\{\begin{array}{l}{5x-3a≥3(x+a)+4}\\{2a-x≥2x-4(a+1)-5}\end{array}\right.$有解且关于x的函数y=(a-1)x2+2$\sqrt{3}$x+a+1与x轴有且只有一个交点的是:-2;
∴使得关于x的不等式组$\left\{\begin{array}{l}{5x-3a≥3(x+a)+4}\\{2a-x≥2x-4(a+1)-5}\end{array}\right.$有解且关于x的函数y=(a-1)x2+2$\sqrt{3}$x+a+1与x轴有且只有一个交点的概率是:$\frac{1}{5}$.
故答案为:$\frac{1}{5}$.
点评 此题考查了概率公式的应用以及不等式组的解集与二次函数的性质.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题
 如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,他先在湖岸上的凉亭A处测得湖心岛上的迎宾槐C处位于北偏东65°方向,然后,他从凉亭A处沿湖岸向正东方向走了100米到B处,测得湖心岛上的迎宾槐C处位于北偏东45°方向(点A、B、C在同一水平面上).请你利用小明测得的相关数据,求湖心岛上的迎宾槐C处与湖岸上的凉亭A处之间的距离(结果精确到1米).
如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,他先在湖岸上的凉亭A处测得湖心岛上的迎宾槐C处位于北偏东65°方向,然后,他从凉亭A处沿湖岸向正东方向走了100米到B处,测得湖心岛上的迎宾槐C处位于北偏东45°方向(点A、B、C在同一水平面上).请你利用小明测得的相关数据,求湖心岛上的迎宾槐C处与湖岸上的凉亭A处之间的距离(结果精确到1米).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | -14 | -7 | -2 | 2 | m | n | -7 | -14 | -23 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
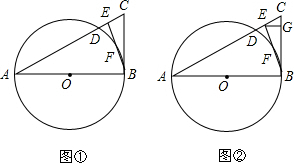
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com