自圆外一点向圆引两条切线所形成的夹角为60°,若切线长为5cm,则此圆的半径为________cm.
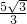
分析:画出几何图形,PA、PB为⊙O的两切线,A、B为切点,∠AOB=60°,PA=PB=5cm,然后连结OP,OA,根据切线长定理得到OP平分∠APB,即∠APO=30°,根据切线的性质定理得到OA⊥PA,然后利用含30度的直角三角形三边的关系求出OA的长即可.
解答:如图,

PA、PB为⊙O的两切线,A、B为切点,且∠AOB=60°,PA=PB=5cm,
连结OP,OA,
∵PA、PB为⊙O的两切线,
∴OP平分∠APB,即∠APO=30°,
∵A为切点,
∴OA⊥PA,
在Rt△OAP中,PA=5cm,∠APO=30°,
∴OA=

=
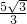
cm.
故答案为
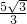
.
点评:本题考查了切线的性质:圆的切线垂直于过切点的半径.也考查了切线长定理以及含30度的直角三角形三边的关系.

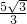
 PA、PB为⊙O的两切线,A、B为切点,且∠AOB=60°,PA=PB=5cm,
PA、PB为⊙O的两切线,A、B为切点,且∠AOB=60°,PA=PB=5cm, =
=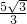 cm.
cm.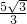 .
.
