
 如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的点,E、G分别是折痕CE与AB、AG与CD的交点.
如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的点,E、G分别是折痕CE与AB、AG与CD的交点. 分析 (1)因为对折,所以∠GAH=$\frac{1}{2}$∠DAC,∠ECF=$\frac{1}{2}$∠BCA,又因为∠GAH=∠ECF,可得AG∥CE,即可得出四边形AECG是平行四边形;
(2)由菱形的定义知可知F,H两点重合,可得出AC=2BC,由此可计算边BC的长.
解答 解:(1)由题意,得∠GAH=$\frac{1}{2}$∠DAC,∠ECF=$\frac{1}{2}$∠BCA,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠DAC=∠BCA,
∴∠GAH=∠ECF,
∴AG∥CE,
又∵AE∥CG
∴四边形AECG是平行四边形;
(2)∵四边形AECG是菱形,
∴F、H重合,
∴AC=2BC,在Rt△ABC中,设BC=x,则AC=2x,
在Rt△ABC中AC2=AB2+BC2,
即(2x)2=62+x2,
解得x=2$\sqrt{3}$(x=-2$\sqrt{3}$舍去),
即线段BC的长为2$\sqrt{3}$cm.
点评 本题考查了翻折变换、平行四边形对的判定、菱形的判定,是一道比较综合的题,难度适中,包含的知识点较多,关键灵活运用矩形的性质.


科目:初中数学 来源: 题型:解答题
 如图,在一条笔直的高速公路I上有A、B两点,点C、D表示两个村庄,相关部门计划在高速公路的AB路段上修建一个收费站E,使得此收费站E到C、D两村庄的距离相等,请你在图中画出收费站E的位置.(保留作图痕迹,不要求写作法)
如图,在一条笔直的高速公路I上有A、B两点,点C、D表示两个村庄,相关部门计划在高速公路的AB路段上修建一个收费站E,使得此收费站E到C、D两村庄的距离相等,请你在图中画出收费站E的位置.(保留作图痕迹,不要求写作法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
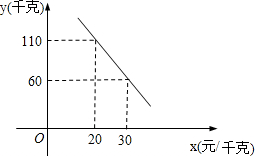 水蜜桃是人们非常喜爱的水果之一,每年七、八月份我市水蜜桃大量上市,今年某水果商以16.5元/千克的价格购进一批水蜜桃进行销售,运输过程中质量损耗5%,运输费用是0.6元/千克,假设不计其他费用.
水蜜桃是人们非常喜爱的水果之一,每年七、八月份我市水蜜桃大量上市,今年某水果商以16.5元/千克的价格购进一批水蜜桃进行销售,运输过程中质量损耗5%,运输费用是0.6元/千克,假设不计其他费用.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 平行四边形AOBC在平面直角坐标系中的位置如图所示,∠AOC=60°,AO=2,AC=4,把平行四边形AOBC绕点O逆时针方向旋转,使点A落在y轴上,则旋转后点C的对应点C′的坐标为(2$\sqrt{3}$,4),(-2$\sqrt{3}$,-4);.
平行四边形AOBC在平面直角坐标系中的位置如图所示,∠AOC=60°,AO=2,AC=4,把平行四边形AOBC绕点O逆时针方向旋转,使点A落在y轴上,则旋转后点C的对应点C′的坐标为(2$\sqrt{3}$,4),(-2$\sqrt{3}$,-4);.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
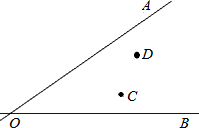 如图所示,107国道OA和320国道OB在某巿相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置.(不写作法,保留作图痕迹,写出结论)
如图所示,107国道OA和320国道OB在某巿相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置.(不写作法,保留作图痕迹,写出结论)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
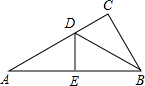 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,沿DE所在直线折叠,使点B恰好与点A重合,若CD=3,AB=8,则DB的值为5.
如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,沿DE所在直线折叠,使点B恰好与点A重合,若CD=3,AB=8,则DB的值为5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 今年“五一”假期,某数学活动小组组织一次登山话动.他们从山脚下点A出发沿斜坡AB到达点B,再从点B沿斜坡BC到达山巅点C,路线如图所示. 斜坡AB的长为1 000米,斜坡BC的长为400米,在C点测得点B的俯角为30°.已知点A的海拔高度为121米,点C的海拔高度为921米.
今年“五一”假期,某数学活动小组组织一次登山话动.他们从山脚下点A出发沿斜坡AB到达点B,再从点B沿斜坡BC到达山巅点C,路线如图所示. 斜坡AB的长为1 000米,斜坡BC的长为400米,在C点测得点B的俯角为30°.已知点A的海拔高度为121米,点C的海拔高度为921米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com