
分析 如图,由AB∥CD,得到△COE∽△AOF,求出$\frac{OC}{AO}=\frac{OE}{OF}$=$\frac{1}{2}$,由于△COD∽△ABO,得到S△COD:S△AOB=($\frac{OC}{OA}$)2=$\frac{1}{4}$,$\frac{{S}_{△AOB}}{{S}_{△ABC}}$=$\frac{2}{3}$,于是得到结论.
解答 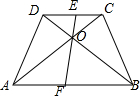 解:如图,∵AB∥CD,
解:如图,∵AB∥CD,
∴△COE∽△AOF,
∴$\frac{OC}{AO}=\frac{OE}{OF}$=$\frac{1}{2}$,
∵△COD∽△ABO,
∴S△COD:S△AOB=($\frac{OC}{OA}$)2=$\frac{1}{4}$,
∴S△COD=$\frac{1}{4}$S△AOB,
∵$\frac{OC}{OA}$=$\frac{1}{2}$,
∴$\frac{OA}{AC}$=$\frac{2}{3}$,
∴$\frac{{S}_{△AOB}}{{S}_{△ABC}}$=$\frac{2}{3}$,
∴S△COD=$\frac{1}{4}×\frac{2}{3}$S△ABC,
∴S△COD:S△ABC=1:6,
故答案为:1:4,1:6.
点评 本题考查了相似三角形的判定和性质,梯形的性质以及三角形面积的计算方法;熟练掌握相似三角形的判定和性质是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | (3,-2) | B. | (-2,-3) | C. | (2,3) | D. | (3,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 砝码的质量x(克) | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 | 600 |
| 弹簧的长度y(厘米) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
| A. | 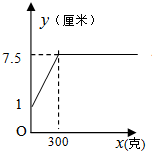 | B. | 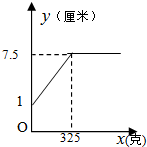 | ||
| C. | 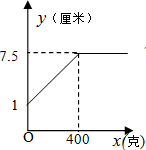 | D. | 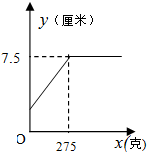 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com