
【题目】如图,矩形ABCD为某中学课外活动小组围建的一个生物苗圃园,其中两边靠墙(墙足够长),另外两边用长度为16米的篱笆(虚线部分)围成.设AB边的长度为x米,矩形ABCD的面积为y平方米.
(1)求y与x之间的函数关系式?(不要求写自变量的取值范围);
(2)求矩形ABCD的最大面积.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】东台教育局为帮助全市贫困师生举行“一日捐”活动,甲、乙两校教师各捐款30000元,已知“……”,设乙学校教师有x人,则可得方程![]() ,根据此情景,题中用“……”表示的缺失的条件应补( )
,根据此情景,题中用“……”表示的缺失的条件应补( )
A. 乙校教师比甲校教师人均多捐20元,且甲校教师的人数比乙校教师的人数多20%
B. 甲校教师比乙校教师人均多捐20元,且乙校教师的人数比甲校教师的人数多20%
C. 甲校教师比乙校教师人均多捐20元,且甲校教师的人数比乙校教师的人数多20%
D. 乙校教师比甲校教师人均多捐20元,且乙校教师的人数比甲校教师的人数多20%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC=4,M为AB的中点.D是射线BC上一个动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED,N为ED的中点,连接AN,MN. 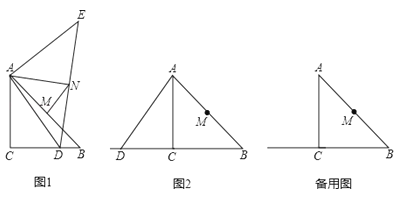
(1)如图1,当BD=2时,AN等于多少?,NM与AB的位置关系是?
(2)当4<BD<8时,
①依题意补全图2;
②判断(1)中NM与AB的位置关系是否发生变化,并证明你的结论;
(3)连接ME,在点D运动的过程中,当BD的长为何值时,ME的长最小?最小值是多少?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( )

A. 第3分时汽车的速度是40千米/时
B. 第12分时汽车的速度是0千米/时
C. 从第3分到第6分,汽车行驶了120千米
D. 从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,过点B作⊙O的切线DE,F为射线BD上一点,连接CF.
(1)求证:∠CBE=∠A;
(2)若⊙O的直径为5,BF=2,tanA=2,求CF的长.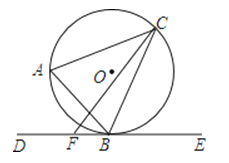
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=3,ON=7,点P是直线OB上的点,要使点P,M,N构成等腰三角形的点P有( )个.
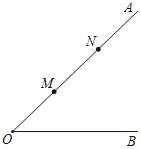
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点O为直线AB上一点,过点O作射线OC,使∠AOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图①中的三角板OMN摆放成如图②所示的位置,使一边OM在∠BOC的内部,当OM平分∠BOC时,∠BON= ;(直接写出结果)
(2)在(1)的条件下,作线段NO的延长线OP(如图③所示),试说明射线OP是∠AOC的平分线;
(3)将图①中的三角板OMN摆放成如图④所示的位置,请探究∠NOC与∠AOM之间的数量关系.(直接写出结果,不须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )

A.100米 B.99米 C.98米 D.74米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com