
| ||
| 2 |


科目:初中数学 来源: 题型:
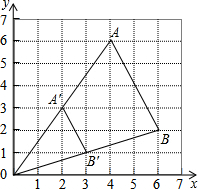 (2013•青岛)如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )
(2013•青岛)如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )查看答案和解析>>
科目:初中数学 来源: 题型:
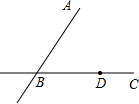 (2013•青岛)已知:如图,直线AB与直线BC相交于点B,点D是直线BC上一点.
(2013•青岛)已知:如图,直线AB与直线BC相交于点B,点D是直线BC上一点.查看答案和解析>>
科目:初中数学 来源: 题型:
| 调查目的 | 了解八年级学生每天干家务活的平均时间 | ||||||||||||||||||||||||||||||
| 调查内容 | 光明中学八年级学生干家务活的平均时间 | ||||||||||||||||||||||||||||||
| 调查方式 | 抽样调查 | ||||||||||||||||||||||||||||||
| 调查步骤 | 1.数据的收集 (1)在光明中学八年级每班随机调查5名学生 (2)统计这些学生2013年4月每天干家务活的平均时间(单位:min)结果如下(其中A表示10min,B表示20min,C表示30min)
以频数分布直方图的形式呈现上述统计结果 请补全频数分布直方图 3.数据的分析: 列式计算所随机调查学生每天干家务活平均时间的平均数(结果保留整数)  | ||||||||||||||||||||||||||||||
| 调查结论 | 光明中学八年级共有240名学生,其中大约有 120 120 名学生每天干家务活的平均时间是20min |
查看答案和解析>>
科目:初中数学 来源: 题型:
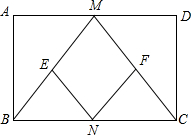 (2013•青岛)已知:如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E,F分别是线段BM,CM的中点.
(2013•青岛)已知:如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E,F分别是线段BM,CM的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com