
【题目】因式分解
(1)a(x﹣y)﹣b(y﹣x)
(2)4x2﹣64
(3)x4﹣18x2+81
(4)81(a+b)2﹣25(a﹣b)2 .
科目:初中数学 来源: 题型:
【题目】为确保广大居民家庭基本用水需求的同时鼓励家庭节约用水,对居民家庭每户每月用水量采用分档递增收费的方式,每户每月用水量不超过基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费.为对基本用水量进行决策,随机抽查![]() 户居民家庭每户每月用水量的数据,整理绘制出下面的统计表:
户居民家庭每户每月用水量的数据,整理绘制出下面的统计表:

(1)为确保![]() %的居民家庭每户每月的基本用水量需求,那么每户每月的基本用水量最低应确定为多少立方米?
%的居民家庭每户每月的基本用水量需求,那么每户每月的基本用水量最低应确定为多少立方米?
(2)若将(1)中确定的基本用水量及其以内的部分按每立方米![]() 元交费,超过基本用水量的部分按每立方米
元交费,超过基本用水量的部分按每立方米![]() 元交费.设
元交费.设![]() 表示每户每月用水量(单位:
表示每户每月用水量(单位:![]() ),
),![]() 表示每户每月应交水费(单位:元),求
表示每户每月应交水费(单位:元),求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)某户家庭每月交水费是![]() 元,请按以上收费方式计算该家庭当月用水量是多少立方米?
元,请按以上收费方式计算该家庭当月用水量是多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P (3, 2),点Q(3, 2),点R(3, 2),点H(3, 2),下面选项中关于y轴对称的是( ).
A. P和Q B. P和H C. Q和R D. P和R
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究同一坐标系中系数互为倒数的正、反比例函数![]() 与
与![]() 的图象性质.小明根据学习函数的经验,对函数
的图象性质.小明根据学习函数的经验,对函数![]() 与
与![]() ,当k>0时
,当k>0时![]() 的图象性质进行了探究,下面是小明的探究过程:
的图象性质进行了探究,下面是小明的探究过程:
(1)如图所示,设函数![]() 与
与![]() 图像的交点为A,B.已知A的坐标为(-k,-1),则B点的坐标为 .
图像的交点为A,B.已知A的坐标为(-k,-1),则B点的坐标为 .
(2)若P点为第一象限内双曲线上不同于点B的任意一点.
①设直线PA交x轴于点M,直线PB交x轴于点N.求证:PM=PN.
证明过程如下:设P(m,![]() ),直线PA的解析式为y=ax+b(a≠0).
),直线PA的解析式为y=ax+b(a≠0).
则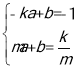 解得
解得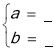
所以,直线PA的解析式为 .
请把上面的解答过程补充完整,并完成剩余的证明.
②当P点坐标为(1,k)(k≠1)时,判断ΔPAB的形状,并用k表示出ΔPAB的面积.
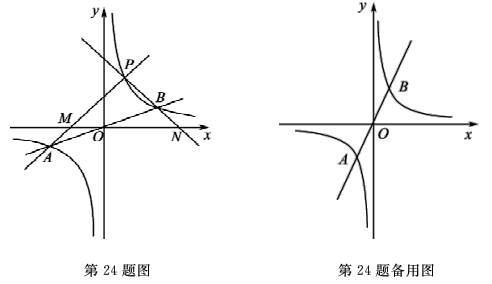
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com