

分析 (1)在图(1)中,过点O作EF∥PB,根据平行线的性质可得出∠GOE=∠P、∠EOB=∠B,结合∠GOB=∠GOE+∠EOB即可证出结论;
(2)结论②正确,由AB∥CD结合(1)结论可得出∠CGO=∠GOB=∠OPB+∠B,根据角平分线的定义可得出∠MGP=$\frac{1}{2}$(∠OPB+∠B)、∠GPQ=$\frac{1}{2}$∠OPB,由GN∥PQ可得出∠NGP=∠GPQ,再根据∠MGN=∠MGP-∠NGP,即可得出∠MGN的度数不变.
解答 (1)证明:在图(1)中,过点O作EF∥PB.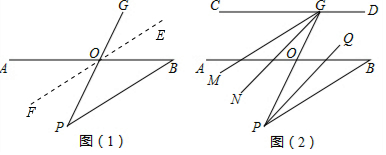
∵EF∥PB,
∴∠GOE=∠P,∠EOB=∠B,
∴∠GOB=∠GOE+∠EOB=∠P+∠B.
(2)解:结论②正确,证明如下:
∵AB∥CD,∠GOB=∠OPB+∠B,
∴∠CGO=∠GOB=∠OPB+∠B.
∵PQ平分∠BPG,GM平分∠CGP,
∴∠MGP=$\frac{1}{2}$CGO=$\frac{1}{2}$(∠OPB+∠B),∠GPQ=$\frac{1}{2}$∠OPB.
∵GN∥PQ,
∴∠NGP=∠GPQ,
∴∠MGN=∠MGP-∠NGP=$\frac{1}{2}$(∠OPB+∠B)-$\frac{1}{2}$∠OPB=$\frac{1}{2}$∠B=15°.
(结论①不正确的理由,随着点G的运动∠CGP是变化的,而∠MGN的度数不变,由此得出结论①不正确)
点评 本题考查了平行线的性质以及角平分线的定义,解题的关键是:(1)利用平行线的性质找出∠GOE=∠P、∠EOB=∠B;(2)根据平行线的性质结合角平分线的定义,找出∠MGN=∠MGP-∠NGP=$\frac{1}{2}$∠B=15°.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:填空题
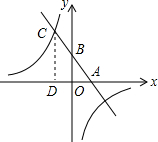 已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数xy=n(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D.若OB=2OA=3OD=6.则反比例函数的解析式为y=-$\frac{20}{x}$.
已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数xy=n(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D.若OB=2OA=3OD=6.则反比例函数的解析式为y=-$\frac{20}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
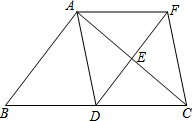 如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.
如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A2旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至得C13,若P(38,m)在第13段抛物线C13上,则m=2.
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A2旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至得C13,若P(38,m)在第13段抛物线C13上,则m=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
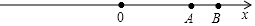 如图,数轴上A,B两点对应的有理数分别为10和15,点P从点B出发,以每秒1个单位长度的速度沿数轴负方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
如图,数轴上A,B两点对应的有理数分别为10和15,点P从点B出发,以每秒1个单位长度的速度沿数轴负方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{10}{3}$a>-$\frac{10}{3}$b | B. | a2>b2 | C. | $\frac{3}{a}$>$\frac{3}{b}$ | D. | -$\frac{1}{5}$+a>-$\frac{1}{5}$+b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{a}{2{b}^{2}}}$=$\frac{1}{2b}$$\sqrt{a}$(b>0) | B. | $\sqrt{\frac{7x}{12{y}^{3}}}$=$\frac{1}{6{y}^{2}}$$\sqrt{21xy}$ | ||
| C. | $\sqrt{{a}^{2}+{b}^{2}}$=a+b(a≥0,b≥0) | D. | 5$\sqrt{\frac{2a}{5}}$=$\sqrt{2a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
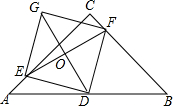 如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.
如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com