
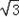 的等边三角形ABC内接于⊙O,点D在
的等边三角形ABC内接于⊙O,点D在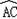 上运动,但与A、C两点不重合,连接AD并延长交BC的延长结于P.
上运动,但与A、C两点不重合,连接AD并延长交BC的延长结于P.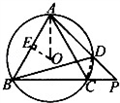
解:(1)过O作OOE⊥于E,连接OA
在Rt△AEO中,∠EAO=30°
AE=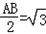
∴
∴OA=2;
(2)连接CD,则∠ABC+∠ADC=180°
又∠ACB+∠ACP=180°,∠ABC=∠ACB=60°
∴∠ADC=∠ACP=120°
又∵∠CAD=∠PAC
∴△ADC∽△ACP
∴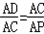
∴AC2=AD·AP
∴y= =
=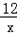 (0<x<2
(0<x<2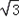 );
);
(3)假设D点在运动的过程中存在这样的位置,使得△DBP成为以DB,DP为腰的等腰三角形,那么DB=DP
∵∠BDC=∠BAC=60°,∠CDP=∠ABC=60°
∴∠BDC=∠CDP
∵CD⊥BP
∴DB是圆的直径,BD=4,DP=4
∵DP=AP﹣AD=y﹣x=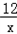 ﹣x=4
﹣x=4
即x2+4x-12=0
∵△=42﹣4 ×(-12)=64>0
∴关于x的方程x2+4x-12=0有两个不相等的实根,说明假设成立
∴x1=2,x2=-6(线段不能为负,舍去)
∴D点在运动的过程中存在这样的位置:即当AD=2时,△BDP成为以BD,PD为腰的等腰三角形。


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
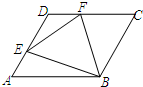 已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.
已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com